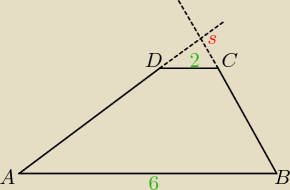
zad matthew: Cześć, mam takie zadanie: Proste zawierające ramiona BC i DA trapezu ABCD przecinają się w punkcie S. Dane są: |AB| = 6, |CD| = 2 oraz obwód trójkąta SCD równy √18. Oblicz obwód trójkąta SAB. Trochę nie wiem jak się za nie zabrać.... Proszę o pomoc...

tim: Masz dwa podobne trójkąty: SDC oraz SAB. Ich podobieństwo to jak |CD| / |AB| = 2/6 = 1/3 Ich obwody są podobne w takiej samej skali √18 / x = 1 / 3 Wylicz x.

miki:

	6
ΔABS ~ ΔSCD w skali k=		= 3
	2

to Ob( ΔABS) = k*Ob(SCD) = 3*√18= 3*3√2= 9√2

miki:

matthew: Dziękuję za odpowiedz Rysunke do zadania drugiego mam jeszcze takie zadanie: wyznacz rownanie okręgu o środku A = (2, 3), stycznego do prostej x − 2x + 1 = 0 zrobilem tak:

	|1*2 + (−2) * 3 + 1|		−5		√5
d =		=		*		= −√5
	√12 +(−2)2		√5		√5

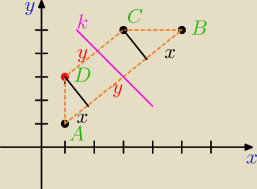
(x −2)² + (y −3)² = −√5 I jeszcze mam takie: Punkty A = (1,1) B = (5,5) i C = (3,5) są wierzchołkami trapezu rownoramiennego ABCD nie bedącego rownoległobokiem, w którym AB || CD. a) wyznacz rownanie osi symetri tego trapezu b)oblicz pole tego trapezu zrobiłem tak: a) A = (1,1), B = (5,5) AB: y = x trapez jest rownoraminny wiec punkt [N{D]] ma taka sama odległośc od punktu A jak punkt C od punktu B, wiec: C = (3,5), D=(1,3) CD: y = x + 2 szukam osi symetrii, czyli prostej k S|DC| = (2,4) S|AB| = (3,3) k: y = −x + 6 b) obliczam długość boku |AB|: d = √(1−5)² + (1−5)² = 4√2 długość boku |DC|: d = √(3−1)² + (1−3)² = 2√2 |DC| = y długość boku |AD| = √(1−1)² + (1 − 3)² = 4 2√2 = 4p8} − 2x 2x = 4√8 − 2√2 x = 2√8 − √2 (2√8 − √2)² + h² = 4² h² = −2 i tutaj się gubię, no bo niemożleiwe jest aby coś podnieść do potęgi wyszła liczba ujemna.... Proszę o pomoc

matthew: ponawiam

matthew: mam jeszcze takie zadanie:

	−x2 + 6x + 21
Funkcja o wzorze f(x) =		opisuje wydajność pracy robotnika w zależności od
	2

czasu pracy x, w ciągu 8−godzinnego dnia pracy, Robotnik rozpoczyna pracę o godz 7.00. O której godzinie jego wydajność jest największa? zrobiłem tak: liczę w przedziale (0,8) dla x = 0, y = 10,5 A(0;10,5) dla x = 8, y = 2,5 B(8;2,5) y_max = 10,5 dla x = 0 odp. o godzinie 10,30 wydajność pracownika jest najwieksza.... Bardzo prosze o sprawdzenie

fragles: odp powinna wyjsc: o godz 10. bo xw=3, i 7(godz o ktorej robotnik zazyna prace) + 3(czas największej wydajności)= 10