Planimetria salamandra: Potrzebuje pomocy z ćwiczeniem 21, chociażby o jakąś wskazówkę, do tej pory wykazałem że kąt MBA = α, a kąt MBO = 2α Zdjęcie: https://imgur.com/a/qmLr6Pw

Mila: Odwróć zdjęcie

salamandra: Proszę: https://imgur.com/a/UG1pFkr

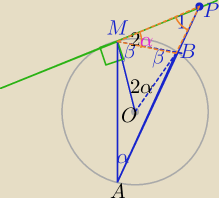
Mila: 1)∡MAB=α ∡BOM=2*∡MAB=2α 2) |∡PMB|=|∡PAM|− kąt między styczną a cięciwą jest równy katowi wpisanemu opartemu na tej cięciwie: ΔBOM− Δrównoramienny ∡2+β=90 2β+2α=180 α+β=90 −−−−−−−−− ∡2+β=α+β⇔ ∡2=α === 3) ΔPMB∼ΔPAM ∡MPB≡∡MPA jako ten sam kąt ∡PMB≡∡MAP⇒∡PMA=∡MBP ⇔ΔPMB∼ΔPAM 4) z(3) mamy:

PM		PB
	=
PA		PM

|PM|²=|PB|*|PA|

salamandra: Dziękuję bardzo W książce mam troche inne twierdzenie nt. kątu między styczną a cięciwą okręgu − "kąt między styczną, a cięciwą okręgu poprowadzoną z punktu styczności jest równy połowie kąta środkowego opartego na łuku, którego końcami są końce tej cięciwy." Nawet dowodziłem tego twierdzenia na lekcji.... https://imgur.com/a/o9kOnwS Mimo to, dziękuję, że zawsze mogę liczyć na pomoc

salamandra: w podpunkcie b) mogę po prostu napisać, że zarówno trójkąt PMB i PAM posiadają kąt α, oraz że "1" jest kątem wspólnym obu trójkąt w związku z tym podobieństwo na mocy cechy kąt−kąt?

salamandra: W sumie bzdurę powiedziałem, bo PMA = α+β, więc tak: MBP = 180−α−"1" oraz PMA = 180−α−"1", więc MBP = PMA