pola gerard: Pole koła opisanego na równoramiennym trójkącie prostokątnymjest równe 9πcm² . Oblicz pole i obwód tego trójkąta.

Blee: 1) masz pole koła −−− wyznacz promień

	1
2) promień =		przeciwprostokątna
	2

3) skorzystaj z tw. Pitagorasa w celu wyznaczenia długości przyprostokątnej 4) oblicz pole i obwód trójkąta

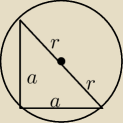
Jerzy: πr² = 9π ⇔ r = 3 d = 2r i d = a√2 teraz oblicz a

gerard: r=3 przeciwprostokątna =6

gerard: a = 3 pierwiastki z 2 ?

Blee: da

gerard: obwód 6 pierwiastków z 2 + 6 ?

gerard: a pole ?

Jerzy: Tak.

Jerzy:

	1
P =		a2
	2

gerard: P = 9 ?

gerard: a nie a * h : 2

Blee: h = a

Jerzy: A ile wynosi h ?

Blee: czemu obwód to 6? skoro trójkąt ma boki równe: 3√2, 3√2, 6

gerard: ale pole = 9 ?

Blee: ach ... 6√2 + 6 napisałeś ... ok

gerard: obwód napisał = 6 pierwiastków z dwóch + 6

gerard: tak

gerard: a pole = 9 ?

Blee: tak

Jerzy: Obwód ma dobry 6√2 = 6 i pole też.

Jerzy: 6√2 + 6 ...miało być.

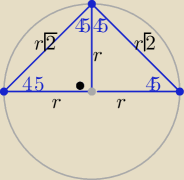
a@b: P_k=πr² ⇒ πr²=9π⇒ r²=9 ⇒ r=3

	1
PΔ=		*2r*r
	2

P_Δ = r²=9 L_Δ=2r+2r√2= 2r(1+√2) L_Δ=6(1+√2)