funkcja kwadratowa z parametrem Nikto0: Witam. Proszę o pomoc . Wyznacz wszystkie wartości parametru m dla których równanie x²−4x=3−m² ma co najmniej jedno rozwiązanie większe od 4 Dlaczego wartość funkcji musi być dodatnia tak jak ktoś napisał tutaj https://forum.zadania.info/viewtopic.php?t=72761 Nie rozumiem tego rozwiązania: https://zapodaj.net/bb637b1b128ab.jpg.html https://zapodaj.net/d1858bf9d8933.jpg.html części od −m²>4 chyba źle jest napisany znak nierówności.

Jerzy: Tam powinno być napisane: "Wartość funkcji dla x = 4 musi być dodatnia", czyli: y(4) > 0

Nikto0: A w rozwiązaniu graficznym co jest nie tak?

Blee: 1) zauważamy, że współczynnik przy najwyższej potędze (przy x²) jest równy a=1 czyli jest dodatni 2) związku z tym −−− będziemy mieli parabole której ramiona są skierowane DO GÓRY 3) jednak bzdurą jest, że x_wierzchołka > 4 4) i także głupotą jest zapisanie, że f(4) > 0 tak naprawdę masz następujące warunki: Możliwość I: a) x_wierzchołka > 4 b) Δ ≥ 0 Możliwość II: a) x_wierzchołka = 4 b) Δ > 0 Możliwość III: a) x_wierzchołka < 4 b) Δ > 0 c) f(4) < 0

Nikto0: A przecież wartość funkcji dla y(4) =−3 czy to nie jest sprzeczność?

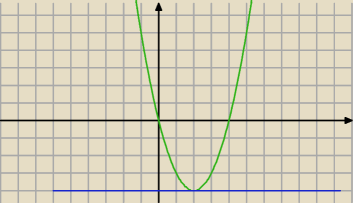
Jerzy: Niebieska prosta ma równanie: y = 3 − m² Mamy więc warunek: y ≥ − 4 , czyli: 3 − m² ≥ − 4 ⇔ −m² ≥ − 7 ⇔ m² ≤ 7

Jerzy: 12:30 , a co zrobiłaś z parametrem m ?

Nikto0: Tak zapomniałam o tym. A jakie rozwiązanie z tego wynika bo ja mam zapisane że ma wyjść m należy do rzeczywistych

Nikto0: Nie rozumiem tego

Jerzy: To moja pomyłka. 12:32 byłoby rozwiazaniem, gdyby w treści zadania było: "ma co najmniej jedno rozwiazanie" i nie byłoby warunku większe od 4

Nikto0: Co mam źle w rozwiązaniu na zdjęciach?

Nikto0: To jakie jest prawidłowe rozwiązanie?

Jerzy: Praktycznie wszystko masz źle. Rozwiazuj tak, jak napisał Blee

Nikto0: Wydaje mi się że w tym momencie mam źle −m²>4 Na początku jest obliczone f(0) które równe jest −3 potem wierzchołek paraboli następnie f(4) obliczone które równa się −3 A teraz nie rozumiem co jest dalej bo mam napisane −m²>4

Blee: Niktro0 −−− wyjaśnij nam Co właściwie chcesz liczyć? W jakim celu liczysz f(0) i niby dlaczego f(0) = −3

Jerzy: A do czego jest ci potrzebne f(0) ? Jak nie rozumiesz czegoś, co sama napisalaś ?

Nikto0: bo f(x)=x²−4x−3 i f(x)=−m²

Jerzy: Najwyrażniej stworzyła dwie funkcje: f(x) = x² − 4x − 3 oraz g(x) = − m², tylko PO CO ?

Jerzy: Zgadnąłem

Nikto0: tak robiliśmy na lekcji

Nikto0: potem chyba trzeba to odczytać z wykresu

Jerzy: To nie jest zadanie do rozwiązywania metodą graficzną.

Blee: ale 'co odczytać' z wykresu

Blee: Tak jak Jerzy napisał. To nie jest tego typu zadanie. Mylisz to zadanie zapewne z: podaj liczbę rozwiązań w zależności od parametru m

Jerzy: 12:32 − tak by wyglądało graficzne rozwiazanie, ale bez warunku "większe od 4 "

Nikto0: Właśnie nie wiem mam napisane −m²>4 m²<−4 m należy do rzeczywistych

Jerzy: Co ty pier...lisz ? Kto ci to napisał ? Sama ? Wypisujesz jakieś brednie i sama ich nie rozumiesz .

Nikto0: źle przepisałam

Jerzy: Co żle przepisałaś ? Treść zadania ?

Nikto0: rozwiązanie zadania.

Nikto0: z tablicy

Jerzy: No to rozwiazuj od poczatku, ale nie twoja metodą, bo jest bez sensu.

Jerzy: Nie wierzę,żeby nauczyciel tak rozwiazywał to zadanie.

Mila: Wyznacz wszystkie wartości parametru m dla których równanie x²−4x=3−m² ma co najmniej jedno rozwiązanie większe od 4 x²−4x−3+m²=0 Δ=28−4m² 1) Δ≥0⇔m∊<−√7,√7> 2) x=2 oś symetrii paraboli x₂>x₁ x₂>4

	4+√28−4m2
x2=
	2

4+√28−4m2
	>4
2

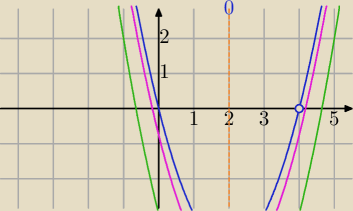
4+√28−m²>8 p{28−4m²>4 /² 28−4m²>16 −4m²+12>0 −m²+3>0 m∊(−√3,√3) i m∊<−√7,√7>⇔ m∊(−√3,√3) Ilustracja m=√3 niebieski m=0 zielony m=−1.5 różowy

Nikto0: Mila z warunku 1) wychodzi mi <−√28,√−28>

salamandra: 28−4m² = 0 −4m² = −28 / (:−4) m² = 7 m = √−7 v m = √7

salamandra: − √7 oczywiście

Nikto0: Dziękuję

Mila: Zgubiłam w jednym zapisie 4 , liczyłam wg . 4+√28−4m²>8