Jasność w punkcie Annnia: Na każdym końcu ulicy o długości a stoi lampa. Jedna lampa jest b³ razy jaśniejsza niż druga. Jakie jest położenie najciemniejszego punktu na ulicy, jeżeli jasność lampy w punkcie jest odwrotnie proporcjonalna do kwadratu jego odległości od lampy? Odpowiedź uzależnij od a i b

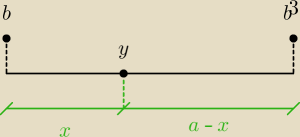
Blee: y − jasność w danym punkcie

	1		1
y = b*(		)2 + b3*(		)2
	x		a−x

szukasz minimum lokalnego tejże funkcji

Annnia: Ale skoro lampa prawa jest b³ razy jaśniejsza to wartości b i b³ nie pasują. Nie powinno być b i b⁴?

Blee: wybacz ... winno być z i z^b4 z −−− jasność 'ciemniejszej' lampy (nie znasz jej jasności)

Blee: z*b³ miało być oczywiście

Annnia: I jak obliczyć minimum jak mam 3 niewiadome?

Blee: a jako, że jasność w (najciemniejszym punkcie) nas nie interesuje ... interesuje nas tylko że w tym punkcie jest najciemniej to możemy sobie przyjąć z=1 (jasność latarni nie jest istotny dla wyznaczenia 'najciemniejszego punktu' − istotna jest 'różnica w jasności' pomiędzy latarniami)

Blee: masz jedną niewiadomą −−− 'x'

Blee: a i b to są PARAMETRY

Blee: a jak zostawiasz 'z' we wzorze ... to 'z' także traktuje jako parametr (który koniec końców powinien i tak się zredukować przy wyznaczaniu 'x' )

Annnia: Dziękuję