Proszę o podpowiedź, jak zabrać się za coś takiego :) Kieubass: Mam problem z dwoma zadaniami, proszę o podpowiedź co tutaj trzeba zrobić 1) Wyznacz te wartości parametru m, dla których zbiór wartości zawiera przedział <−1, 1>?

x2 + m2
	> 1
2m(x+6)

2) Dla jakich wartości parametru m nierówność jest tożsamościowa w R?

x2 − mx +1
	> −3
x2 + x + 1

W zadaniu pierwszym wyznaczyłem dziedzinę, że m różne od zera oraz x różne od −6. Następnie pomnożyłem stronami przez kwadrat mianownika i przerzuciłem na lewą stronę dostając: (x² + m²)m(x+6) − 2m²(x+6)² >0 Wyłączyłem wspólny czynnik przed nawias, a to co z tego powstało uprościłem: m(x+6)(x² − 2mx + m² − 12m) >0 Niestety nie wiem czy jest sens liczyć deltę z tego ostatniego nawiasu, a nawet jeśli podam rozwiązania, to nie wiem czy coś mi to da...

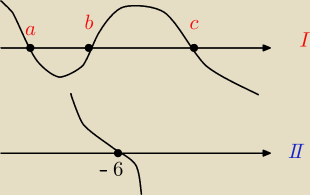Blee: dla m > 0 (rys I) Δ = 4m² − 4m² + 48m = 48m √Δ = 4√3m x₁ = m − 4√3m x₂ = m + 4√3m w takim razie x₁ < −1 ∧ x₂ > 1 m − 4√3m + 1 < 0 ∧ m + 4√3m − 1 > 0 rozwiązujesz te dwie nierówności Uwaga c = x₂ (ponieważ x₂ > x₁ oraz x₂ > 0 > −6) b = x₁ lub b = −6 (jeżeli x₁ < −6) a = −6 lub a = x₁ (jeżeli x₁ < −6) nie jest to aż tak bardzo istotne −−− bo jeżeli nawet x₁ < −6 ... to i tak <−1;1> ∊ (−6 , x₂) jeżeli tylko x₂ > 1 dla m < 0 (rys II) m(x+6)x² > 0 <−−− jedyne miejsce zerowe to x = −6 czyli nie ma możliwości aby x∊<−1;1> mógł spełnić tą nierówność

Blee: 2) w drugim zadaniu zauważ, że: x² + x + 1 > 0 dla dowolnego x∊R więc mamy nierówność: x² − mx + 1 > −3x² − 3x − 3 4x² + (3−m)x + 4 > 0

	3−m
x2 +		x + 1 > 0 będzie to spełnione dla dowolnego x jeżeli Δ < 0
	4

	3−m
czyli (		)2 < 4
	4

rozwiązujesz