Premutacje bez powtorzeń 6latek: Spotkało się 10 osób Ile jest sposobów zajęcia miejsc przy okrągłym stole przez te osoby ? Założmy że wszystkie osoby usiadły przy stole Rozwiażazanie tego zadania zależy od sprecyzowania jakie dwa rozmieszczenia przy stole uznamy za rozne Możliwe są dwa przypadki A) Conajmniej dwie osoby będą siedziały na innych krzesłach . Takich ustawień jest tyle ile ustawień 10 osób w szeregu czyli 10! B) Conajmniej jedna osoba zmieniła swoich sąsiadów (oznacza to np., że jeżeli wszyscy przesiąda sie o jedno miejsce w prawo to każdy siedzi na innym krześle , a mimo tego nie otrzymujemy nowego rozmieszcenia osób przy stole) Wówczas rozwiazaniem zadania jest liczba 9! Uzasadnij to dokładnie Są to permutacje bez powtorzeń

Blee: Ale co należy konkretnie uzasadnić

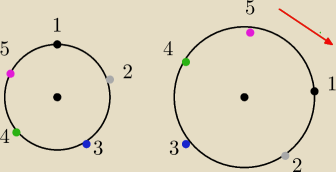
6latek: To jedno z mozliwych ustawien narysowalem dla 5 osob

6latek: Ze wowczas rozwiazaniem zadania jest 9! a nie 10! To jest z ksiazki Kurczab Swida klasa 3

Blee: (A) krzesła ponumerowane ... dlatego mamy 10! możliwości ustawienia (B) krzesła NIE SĄ ponumerowane dlatego każde przesunięcie sekwencji (abcdefghij) oznacza to samo , więc wynik z (A) należy podzielić przez 10 ... więc otrzymujesz 9! możliwości

6latek: Wlasnie ja to B) nie rozumiem Dlaczego mam podzielic przez 10 (tutaj bo 10 osob)

Blee: Inna możliwość 'rozumowania' (B) krzesła nie są ponumerowane ... więc pierwsza osoba siada na dowolnym krześle na 1 SPOSÓB (bo wszystkie krzesła są dokładnie takie same). Gdy już usiadł to sytuacja przy stole się zmienia −−− ta osoba staje się 'punktem odniesienia' względem pozostałych krzeseł (np. krzesło X to trzecie krzesło na 'na lewo' od siedzącego), więc następny człowiek ma do wyboru 9 możliwości (bo każde krzesło stało się 'wyjątkowe i jedyne w swoim rodzaju względem pierwszego siedzącego' ). I stąd masz 1*9! = 9!

6latek: Na razie dziękuje . Zobaczymy jak pójda zadania .

Jerzy: Wyobraż sobie,że 12:15 przecinasz lewy okrag i prostujes go w odcinek i niech to bedzie ławka. Na tej ławce mozesz posadzić 5 osób na 5! sposobów. No ale masz 5 mozliwosci przeciecia tego okregu , więc powstałe prmutacje liczysz pieciokrotnie,

	5!
czyli musisz 5! podzielis przez 5 , a stąd:		= 4!
	5

Jesli zatem krzesła nie są numerowane, to n osob przy stole rozmieszczasz na (n − 1)! sposobów. Jesli są ponumerowane, to daną permutację mozesz "obrócić" wokół stołu 5 razy, czyli4!*5 = 5!

6latek: Dziękuje Ci bardzo Jerzy