Zadanie student: Zastanawia mnie jedna rzecz odnośnie iloczynu skalarnego Dla przykładu 2 wektory: a↑ = 2i + 3j b↑ = −1i +2j a↑◯b↑ = 2i◯(−1)i + 2i◯2j + 3j◯(−1)i + 3j◯2j ostatni składnik: 3j◯2j wartość pierwszego wersora 3, drugiego 2 żaden ∡ między nimi nie występuje, cos(0) = 1 więc 3j◯2j = 3*2 = 6 pierwszy składnik: 2i◯(−1)i wartość pierwszego wersora 2, drugiego |−1| = 1 2 wersory tego samego kierunku ale o przeciwnym zwrocie, ∡ między nimi powinien wynosić π w konsekwencji czego dla cos(π) = −1 wynikiem będzie |2|*|−1|*(−1) = 2, co jest nieprawdą Czy to jest jakaś konwencja, że dla każdej pary wersorów, posiadających ten sam kierunek ( niezależnie od zwrotu ), to kąt między nimi zawsze będzie wynosić 0? Przyjęło się tak na poczet prawidłowości wzoru?

Pytający: |2|*|−1|*(−1) = −2

student: Zjadło minusa

Pytający: Znaczy jednak wszystko się zgadza?

Adamm: Jak wolisz to może wynosić 2π lub 4π lub ...

student: Innymi słowy, ∡ między wektorami wynoszący π nie istnieje dla iloczynu skalarnego?

Adamm: excuse me?

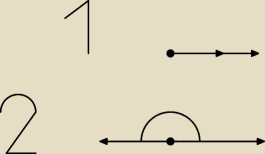
student: Inaczej... Jaki jest kąt w 1 i 2 przypadku?

student: To jak to w końcu jest, w drugim π czy 0?

Adamm: π

nazwą: <n Tak by się wydawało... a z definicji dla iloczynu skalarnego wychodzi, że taki ∡ nie istnieje

student: Więc konwencja czy luka w definicji?

student: Żadna luka tylko błąd w książce... Można spać spokojnie