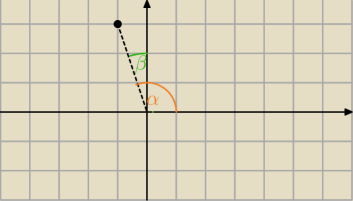
Na końcowym ramieniu kąta alfa.. studentX: Na końcowym ramieniu kąta α... https://imgur.com/sy9rr4H Myślałem, że rozumiem to zadanie, ale podczas rozwiązywania nie jestem pewien wyniki. Proszę o weryfikację. Zacząłem od wyznaczenia kąta dopełniającego kąt α do tych 180 stopni. Nazwijmy go β tgβ = 3/1 = 3 β = 135 stopni (? tu zaczęły się moje wątpliwości).

Blee: po co masz punkt P(−1,3); α ∊ (90^o ; 180^o) więc: sinα > 0 cosα < 0 więc:

	1		−3		3
sinα*cosα =		*		= −
	√1+9		√1+9		10

Blee: druga sprawa −−−− β = 135 = 90 + 45 ... więc nie ... na pewno tgβ ≠ 3

studentX: Dzięki wielkie! Mógłbyś powiedzieć mi słowo o tym, dlaczego możemy liczyć sinα jako 3/√10, skoro np. 3 nie leży na przeciw kąta α tylko na przeciw (180 stopni − α)? Jestem za głupi

Blee: sin α = sin(90+β) = sinβ cos α = cos(90+β) = −cosβ wzory redukcyjne się kłaniają

studentX: o chuj XD DZIĘKI

Jerzy: @Blee , coś te wzory z 12:04 są " nie bardzo"

Blee: masz rację