Granica ciągu __:

	4π
limn→∞(sin		n)
	n

Dzień dobry! Jakby Państwo rozwiązali tę granicę bez użycia reguły de l`Hospitala i bez korzystania z zapisu sin i cos w postaci szeregów?

ABC:

	4π
podstawienie n=
	t

__: @ABC

	sin(t)
Co zostawia nas z problemem wykazania limt→0		=1, gdzie t = 4nπ, n∊ℕ
	t

ABC: ten problem da się rozwiązać bez rzeczy które wymieniłeś 16:53

Inka:

	sin(t)
Korzystajac z nieskonczenie malych gdy t→0 z automatu limt→0		=1
	t

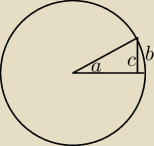
__: Z pewnością Ale nie wiem jak to zrobić w jakiś ścisły sposób. (Znalazłem argument oparty na tym, że dla małego kąta a, długość odcinka c staje się bliska długości łuku b, ale to nie jest raczej ścisłe podejście)

__: @Inka Mogłabyś rozwinąć? Bo na tę chwilę niestety nie rozumiem

ABC: masz dowód z tw o 3 ciągach w Fichtenholzu, korzysta z teorii miary w sposób ukryty, ale do tak poważnej granicy z czegoś trzeba skorzystać

__: @ABC Dziękuję, zajrzę