Zbiory nieskończone podstawy Jan: Witam Mam taki przykład który polega na obliczeniu sumy oraz iloczyny nieskończonego zbioru t należy do dodatnich rzeczywistych(zakładamy że 0 również należy)

	1
A = {x : 0 < x <=		}
	t+1

otrzymałem taki wynik: suma (0,1> iloczyn zbiór pusty Czy mógłbym prosić o potwierdzenie prawdziwości wyniku lub ewentualną korektę

ite: Tu chodzi o rodzinę zbiorów A_t?

ite: Możesz wpisać polecenie do zadania?

Jan: Wyznacz sume oraz iloczyn dla rodzin zbiorów (zakładamy, że 0 nalezy R+):

Jan: A_t ∊ R⁺

Jan:

	−1		1
do tego w przykładzie At = { x :		< x <
	t+1		t+1

otrzymałem wyniki : suma = liczby rzeczywiste iloczyn = {0}

ite: t∊R₊∪{0}

	1
A0 = {x : 0<x≤		}
	1

	1
A1 = {x : 0<x≤		}
	2

	1
A2 = {x : 0<x≤		}
	3

... U^∞ A_t=(0,1> t=0 ∩^∞ A_t=∅ t=0

ite: Zapis z 13:35 do czego sie odnosi? Dla rodziny zbiorów z 13:43 t należy do jakiego zbioru?

Jan: W poleceniu było podane że w każdym przykładzie t należy do zbioru R⁺ zapomniałem dopisać w 13:29 13:43 R⁺

ite: To w tym pierwszym przykładzie też t należy do R₊? Więc nie jest prawdą, to co napisałam, że t∊R₊∪{0}. Wtedy nie istnieje A₀ i suma jest inna.

Jan: Tak dla obu przykładów R₊. Czyli jakby to wyglądało

Jan: Ale w poleceniu było podane że przyjmujemy 0 jako R₊

Jan: Czyli nasze wyniki się pokrywają

ite: Dlatego chciałam, żebyś podał polecenie do zadania a nie luźny opis.

Jan: Przepraszam mój błąd strasznie chaotycznie to opisałem, czy mógłbym prosić również o sprawdzenie przykładu 2

ite: więc nadal zakładam, że t∊R₊∪{0} 13:43 Dla jakiej wartości t do zbioru A_t bedzie należeć np.1000? Piszesz, że sumą tej rodziny zbiorów jest zbiór liczb rzeczywistych R, więc taki zbiór musi istnieć.

Jan: Faktycznie rozpisałem dla większych liczb i wychodzi na to że im wieksza wartośc tym bliżej 0 czyli wychodzi na to że suma będzie zbiorem liczb ( −1 , 1)

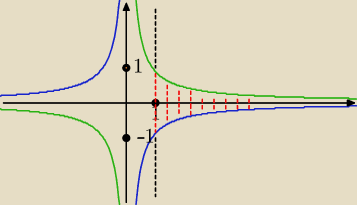
ite: Suma sie zgadza, iloczyn też.

	−1		1
Można pomocniczo spojrzeć na wykresy y=		i y=		narysowane w jednym układzie
	x+1		x+1

współrzędnych.

Jan: A czy mógłbym jeszcze prosić o pomoc z czymś takim bo nie za bardzo wiem jak się za to zabrać (x,y) : x 2 + y 2 <= t² założenia i polecenie tak jak wcześniej

ite: Źle na tym wykresie narysowałam oś rzędnych, ale chyba widać wartości.

ite: Zapis (x,y) oznacza przedział? Chodzi o sumę i iloczyn przedziałów? Nie wiem, jak odczytać x 2 + y 2 x*2 + y*2 czy x² + y² ? ? ?

Jan: A_t = {(x,y) : x² + y² <= t²} sumę oraz iloczyn jak poprzednio

ite: Czy x,y∊ℛ ?

Jan: Nie mam podane wiadomo tylko że t ∊ R₊ wraz z 0 wiadomo tylko że x,y są takię że x² + y² <= t²

Jan: rozrysowałem w wolframie wydaję mi się że suma to będzie R² a iloczyn (0,0) (jako punkt) jednak nie wiem czy takie rozumowanie wystarczy

ABC: ja bym ci kazał udowodnić rozpisując dwie inkluzje

Jan: Dopiero teraz zauważyłem że to przecież równanie koła

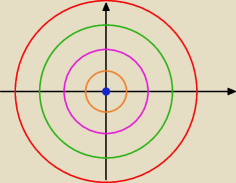
ite: Zgadza się. Można to tak przedstawić, że pary liczb spełniające tę nierówność będą należeć do takich kół. A₀={(0,0)} Tylko para (0,0) spełnia nierówność x²+y²≤ t² dla każdego t∊R₊∪{0}. Więc iloczynem jest zbiór {(0,0)}. Dla każdej pary liczb rzeczywistych (x,y) można znaleźć takie t, że warunek x²+y²≤ t² będzie spełniony. Więc do sumy należy każda para.

Jan: Bardzo dziękuję za pomoc <3

ite: ABC wystarczy tak, jak napisałam? Czy to za mało?

ABC: ja bym zażądał wyjaśnienia dlaczego para inna niż (0,0) nie należy do części wspólnej, mianowicie aby delikwent wskazał zbiór do którego taka para nie należy

ite: dzięki