geometria analityczna Kasia: Punkt P=(−2,2) jest środkiem symetrii rombu ABCD, w którym (wektor)AC = [12,6] i wektor(AB) || k : y=−1/2x−1; Wyznacz B(xb,yb) i D(xd,yd); Potrzebuję pomocy, nie mam pojecia jak sie za to zabrać Z góry dziękuję za pomoc

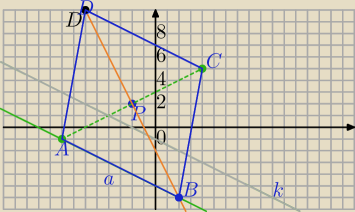
Mila: Zaczynamy od rysunku: 1) AC ^→= [12,6] P=(−2,2) P=(−2,2)→T_[6,3}⇒C=(−2+6,2+3)=(4,5) P=(−2,2)→T_[−6,−3}⇒A=(−8,−1) 2) AB||k

	1
k: y=−		x−1
	2

Prosta AB:

	1		1
a: y=−		x+b i A∊a⇔ −1=−		*(−8)+b
	2		2

b=−5

	1
a: y=−		x−5
	2

3) Prostopadłą do AC: BD^→⊥AC Równanie prostej : 12(x+2)+6*(y−2)=0 /: 6 2(x+2)+y−2=0 2x+y+2=0 y=−2x−2 4) Punkt przecięcia prostych BD i a:

	1
−2x−2=−		x−5
	2

x=2, y=−6 B=(2,−6) D=? oblicz sama

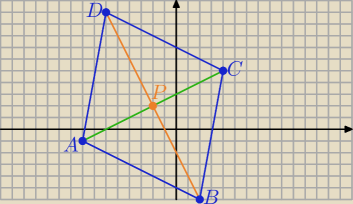
Eta: → AP=[6,3] to A( −2−6, 2−3) =(−8,−1) i C(−2+6, 2+3)= (4,5)

	1
prosta AB : y= −		(x+8)−1
	2

	1
AB: y=−		x−5
	2

prosta BD : 6(x+2)+3(y−2)=0 ( bo jest prostopadła do AC BD : y=−2x−2 Rozwiąż układ równań danych prostymi : AB i BD otrzymasz B(....., ....) D(....., .....) wyznacz korzystając z tego, że P jest środkiem odcinka BD dokończ obliczenia Odp: B(2, −6) , D(−6,10)

Eta: "daremne żale, daremny trud..."