Odcinek o końcach A (-1,-3), B(3,5) jest średnicą pewnego okręgu. Czarniecki: Odcinek o końcach A (−1,−3), B(3,5) jest średnicą pewnego okręgu. Punkt C należy do tego okręgu i jest jednakowo oddalony od punktów Ai B. Oblicz współrzędne punktu C i pole trójkąta ABC. Doszedłem do tego, że połowa AB, to promień, czyli R=2√5. Następnie policzyłem środek odc. AB, S=(1,1), wyznaczyłem wzór odcinka AB, y=2x−1, wyznaczyłem wzór jego symetralnej: y=−1/x + 3/2. Oznaczyłem punkt C jako (x, −1/2x+3/2), a następnie podstawiłem do wzoru r=CS, ale nie wyszedł mi wynik. Użyłem jakiegoś złego sposobu, czy pomyliłem się w obliczeniach?

Inka: 1) Zrobic rysunek (szkic 2) napisac rownanie tego okregu 3) napisac rownanie symetralnej AB 4) policzyc punkty przeciecia sie okregu i symetralnej (beda dwa 5) policzyc pole trojkata

Czarniecki: Proszę jednak o rozpatrzenie mojego sposobu

Inka: To pokaz obliczenia od momentu Oznaczylem punkt C jako itd

Czarniecki: r²=(x−1)²+(1/2−1/2*x)² x²−2x+1+1/4−1/2*x+1/4x²=20 5/4x²−3/2x+5/4=20 /*4 5x²−6x−75=0 Delta, która z teog wychodzi nie daje żadnych wyników

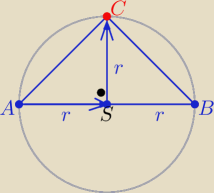
Eta: Proponuję rozwiązanie z wykorzystaniem wekorów P(ABC)=r² =20 i S(1,1) → → AS=[2,4] ⊥ CS to CS= [−4,2] lub [4,−2] , CS=[1−x, 1−y] to: 1−x=−4 i 1−y=2 ⇒ x=5 i y=−1 lub 1−x=4 i 1−y=−2 ⇒ x=−3 i y=3 C(5,−1) lub C(−3,3) ================

Eta: Masz błędne równanie prostej AB ( AB : y= 0,5x−2,5 a_AB=1/2 to a_SC=−2 SC: y=−2x+3

Czarniecki: Znam inne sposoby rozwiązania, ale chodzi mi o ten, przeze mnie przedstawiony.

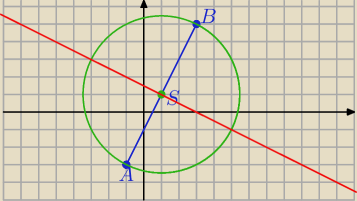
Mila: A (−1,−3), B(3,5) 1) S=(1,1) r=2√5 (x−1)²+(y−1)²=20 równanie okręgu. 2) punkt C leży w punkcie przecięcia symetralnej AB i okręgu symetralna AB: (x+1)²+(y+3)²=(x−3)²+(y−5)²

	1		3
y=−		x+
	2		2

podstawiamy do równania okręgu:

	1		3		1		1
(x−1)2+(−		x+		−1)2=20⇔(x−1)2+(−		x+		)2=20
	2		2		2		2

	1		1		1
x2−2x+1+		x2−		x+		=20
	4		2		4

5		5		75
	x2−		x−		=0 /*4
4		2		4

5x²−10x−75=0 x=3 lub x=5 y=.. licz dalej sam

Czarniecki: 5=3a+b oraz −3=−a+b Z drugiego równania: b=a−3 − wstawiamy do pierwszego: 5=3a+a−3 4a=8 a=2, gdzie tu błąd?

Eta: Widzicie "przewagę" metodą wektorów ?

Czarniecki: Mila Dokładnie o to mi chodziło, dziękuję. Teraz widzę, że jedną rzecz źle dodałem

Inka: Do wyznaczenia rownania symetralnej niepotrzebny jest caly wzor prostej AB wystarczy jej wspolczynnik kierunkowy

Czarniecki: Eta Z wektorami wszystko jest prostsze, np wzór na pole: 1/2 | wyznacznik 2 wektorów |, którego o dziwo nie ma w programie nauczania

Eta: W tym przypadku : P=r² ( i nie trzeba wektorów

Czarniecki: Wiem, wiem. Tak ogólnie mówię

Eta: U Mili 5x²−10x−75=0 x= 5 v x= −3

Mila: Tak, x=−3 . Dziękuję za poprawę.