W trójkącie ABC dane są wierzchołki A(-2,-2) i B(6,0) Czarniecki: W trójkącie ABC dane są wierzchołki A(−2,−2) i B(6,0). Środkowa CS jest równa 7√2 i zawiera się w prostej y=−x+1. Wyznacz równanie prostej zawierającej wysokość opuszczoną z wierzchołka C. Wyznaczyłem równanie prostej AB=1/4x−3/2, współrzędne środka tego boku, S=(2.−1), ale mam problem z wyznaczeniem współrz. pkt C=(xc; −xc+1). Podstawiam ten punkt do wzoru na odległość i wychodzi, że xc=3√5, co jest niezgodne z odpowiedzią.

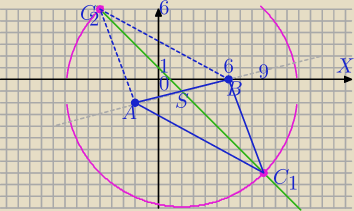
Mila: s: y=−x+1 A(−2,−2) i B(6,0) 1) prosta AB: y=ax+b

	1		1		3
a=		i 0=		*6+b⇔b=−
	4		4		2

	1		3
y=		x−
	4		2

S=(2,−1) 2) C=(x,y) (x−2)²+(y+1)²=(7√2})² i y=−x+1 (x−2)²+(−x+2)²=98 2(x−2)²=98, (x−2)²=49 x−2=7 lub x−2=−7 x=9 lub x=−5 y=−9+1 ⇔C₁=(9,−8) lub y=5+1 ⇔C₂=(−5,6) dalej sam

Czarniecki: (x−2)²+(−x+2)²=98 2(x−2)²=98, Przecież (x−2)², nie jest równe (−x+2)²,

ICSP: jest

Czarniecki: Racja. Dziękuję