kombinatoryka
lola456: Witam, mam zadanie z kombinatoryki do rozwiązania.
Na ile sposobów można ustawić w kole trzy małżeństwa tak, aby nikt nie stał obok
swojego małżonka?
Zastanawiam się czy użyć tutaj metody włączania i wyłączania ale nie wiem do końca jak to
ugryźć. Proszę o pomoc
8 lis 22:56
jc: Dla 3 małżeństw można zwyczajnie.
Mamy 2 schematy:
C B
A A
B C
oraz (3 razy)
B C
A A
B C
Każdy schemat możemy wypełnić na 23*3! sposobów.
Razem 4*6*8.
A jeśli liczy się kto koło kogo siedzi i po jakiej stronie siedzi, dzielimy wynik przez 6.
8 lis 23:09
Blee:
wszystkich ustawień masz 5!
ustawień, że wszystkie trzy małżeństwa są obok siebie masz: 24
ustawień, że dokładnie dwa małżeństwa są obok siebie masz: 23
ustawień, że dokładnie jedno małżeństwo jest obok siebie masz: 3*24
8 lis 23:12
Blee:
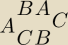
jc −−− a czemu przyjąłeś że masz punkt odniesienia

I to nie są wszystkie schematy
chociażby takiego nie masz
8 lis 23:15
jc: Uwzględniłem. Litery mówią tylko, co z czym połączyć.
8 lis 23:35
jc: Inaczej.
Wszystkie ustawienia: 6!
Pierwsza para obok siebie: 6*2*4!
Pierwsza i druga: 6*3*4*2
Każda: 6*8*2
wynik/6 = 120 − 3*48+3*24−16=32
Tak czy owak 32.
8 lis 23:42
Blee:
Ponownie pytam −−− dlaczego zakładasz z góry że masz punkt odniesienia dla tego okręgu?
Przecież jest to zadanie typu: 'przy okrągłym stole siadają ludzie'
Gdyby to była kwestia policzenia prawdopodobieństwa, to wsio ryba ... ale tutaj sprawa inaczej
wygląda.
Tak więc − nie powinno się mówić o tym, że wszystkich ustawień jest 6!
8 lis 23:48
jc: Na koniec dzielę przez 6.
8 lis 23:54
lola456: A wiecie jak zrobić to samo tylko korzystając z zasady włączania i wyłączania?
9 lis 17:23
jc: o 23:42 zastosowałem zasadę włączania wyłączania.
Szukasz |Ω−AUBUC|, gdzie A − pierwsza para siedzi koło siebie,
B − druga para siedzi koło siebie, C − trzecia para siedzi koło siebie.
Ω to wszystkie możliwości. Łatwiej myśleć, że miejsca są ponumerowane, a na koniec
wynik podzielić przez 6.
|Ω|=6!, |A|=|B|=|C| = 6*2*4!, |AB|=|BC|=|AC|= ..., |ABC| = ...
9 lis 17:47
lola456: Dziękuję bardzo za odpowiedź

10 lis 22:22
lola456: Jeszcze raz wrócę do tego zadania, bo już nie wiem która metoda jest poprawna czy ta z 5! czy
ta z 6!?
14 lis 13:42
jc: To zależy jakie sytuacje utożsamiasz.
Możesz myśleć, że masz ponumerowane miejsca. Możesz myśleć, że cykliczne przesunięcie
nic nie zmienia, a możesz też myśleć, że symetryczne ustawienie jest tym samym,
co oryginalne.
Ja bym zaczął o 6! i ewentualnie podzielił wynik przez 6 lub nawet 12.
14 lis 14:56
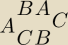 jc −−− a czemu przyjąłeś że masz punkt odniesienia
jc −−− a czemu przyjąłeś że masz punkt odniesienia  I to nie są wszystkie schematy
chociażby takiego nie masz
I to nie są wszystkie schematy
chociażby takiego nie masz
