Kule i szuflady
Kaśka: Na ile sposobów możemy umieścić 8 kul (4 białe, 4 czarne) w ośmiu szufladach, tak aby biała
kula nie była koło innej białej kuli?
Każda szuflada pomieści tylko jedną kule. Czarna kula może być w szufladzie koło czarnej kuli.
Szuflady są ułożone w jednym rzędzie. Jeśli to nie problem porszę o wytłumaczenie

7 lis 20:11
Pytający:
Biała nie może sąsiadować z białą, więc z automatu musisz dać po 1 czarnej między białe, wtedy
masz:
○●○●○●○
i pozostaje Ci 1 czarna do dorzucenia. Zauważ, że po dorzuceniu będziesz już miała ułożenie w
rzędzie odpowiadające rozłożeniu kul (po jednej) w szufladach. Pozostaje pytanie: na ile
sposobów możesz dorzucić tę czwartą czarną kulę, coby otrzymać różne rozmieszczenia?
7 lis 21:00
Kaśka: Na 5?
7 lis 21:06
PW:
zacznijny od umieszczenia kul czarnych w szufladach nr 4 i nr 5. Jak łatwo zauważyć, jedyną
możliwością rozmieszczenia kul białych jest włożenie ich do szuflad o numerach 1, 3 oraz 6, 8.
Co będzie, jeżeli do szuflad 4. i 5. włożymy kule białą i czarną?
7 lis 21:08
PW: Przepraszam, nie widziałem odpowiedzi Pytającego..
7 lis 21:10
Pytający:
Kaśka, tak jest 5 takich sposobów.
PW, nie szkodzi.

7 lis 21:17
PW: 
Oczywiście taki sposób rozumowania znam, ale chciałem zainspirować
Kaśkę do innego.
7 lis 21:19
Kaśka: No tak, ale pierwsza Biała kula może być w czterech miejscach, potem drugiej zostają trzy
itd... wydaje mi się, że będzie więcej sposobów
7 lis 21:22
Kaśka: Nie wiem, czy dobrze myślę
7 lis 21:25
Mila:
7 lis 21:37

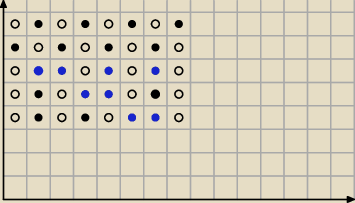
 zacznijny od umieszczenia kul czarnych w szufladach nr 4 i nr 5. Jak łatwo zauważyć, jedyną
możliwością rozmieszczenia kul białych jest włożenie ich do szuflad o numerach 1, 3 oraz 6, 8.
Co będzie, jeżeli do szuflad 4. i 5. włożymy kule białą i czarną?
zacznijny od umieszczenia kul czarnych w szufladach nr 4 i nr 5. Jak łatwo zauważyć, jedyną
możliwością rozmieszczenia kul białych jest włożenie ich do szuflad o numerach 1, 3 oraz 6, 8.
Co będzie, jeżeli do szuflad 4. i 5. włożymy kule białą i czarną?

 Oczywiście taki sposób rozumowania znam, ale chciałem zainspirować Kaśkę do innego.
Oczywiście taki sposób rozumowania znam, ale chciałem zainspirować Kaśkę do innego.
