Trapez Kamil: odcinek łączący środki dwóch sąsiednich bokow trapezu równoramiennego dzieli jego pole w stosunku 1:3. Jaki jest stosunek długości podstaw tego trapezu ?

Kamil: Mógłby ktoś chociaż podać jakąś wskazówkę

Mila: Dane chyba się nie zgadzają. Na pewno ma być 1:3 ?

Kamil: 1:9 tak mój błąd

Kamil: Z czego skorzystać? Spróbuję sam, ale zupełnie nie wiem jak się do tego zabrać.

Saizou :

	H
sinα =
	2c

	h
sinα =
	c

H		h
	=
2c		c

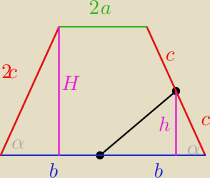
H=2h

	1
Ptrapezu=		(2a+2b)*H=(a+b)*2h
	2

	1
Pmałego trójkąta=		h*b
	2

za zależności stosunku 1:9 mamy P_trapezu=10*P_{małego trójkąta}

	1
(a+b)*2h=10*		*h*b
	2

a+b=5b a=4b

a		1
	=
b		4

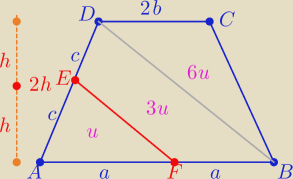
Eta: Z podobieństwa trójkatów AEF i ABD w skali k=2 P(AEF)=u to P(ABD)=4u więc P(EFBD)=3u to P(BCD)=6u ( jak na rysunku

	a*h
P(AEF)=		=u ⇒ a*h=2u
	2

	2b*2h
P(BCD)=		=6u ⇒ b*h=3u
	2

ah		2u
	=
bh		3u

	a
		=2:3
	b

=========

Eta: No i............

Mila: Już piszę.

Eta: Po co? ja już napisałam

Saizou : Poprawiam moją "końcówkę"

	1
(a+b)*2h=10*		*h*b
	2

2a+2b=5b 2a=3b

a		3
	=
b		2

Eta: Dla jasności : U Saizou dolna podstawa 2b u mnie 2a górna podstawa 2a u mnie 2b

	b		a
zatem wynik :		= 2:3 i u mnie		=2:3
	a		b

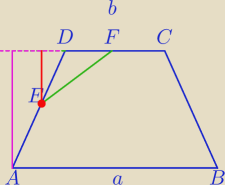
Mila: Bez wykorzystania .podobieństwa 1)

	1
PDFE=		b*h
	8

	a+b		1		4a+3b
P{ABCFE}=		*h−		b*h=		*h
	2		8		8

2}

1   b*h 8		1		b		1
	=		⇔		=
4a+3b   *h 8		9		4a+3b		9

9b=4a+3b 6b=4a

b		2
	=
a		3

===========

Eta:

Mila: Dla ucznia VII klasy. 1)

	1
PDFE=x, x=		b*h
	8

P_ABCFE=9x z treści zadania 2)

	a+b
PABCD=10x ⇔10x=		*h⇔
	2

	a+b
x=		*h
	20

Porównanie:

a+b		b
	*h=		*h
20		8

a+b		b
	=
20		8

8a+8b=20b⇔8a=12b /:4 2a=3b

b		2
	=
a		3

========

Cy-57MAKS: A dla przedszkolakow Milu tez poprosze

Mila: To jest zadanie z konkursu dla uczniów VIII klasy. Dla przedszkolaków będzie kolaż.

Cy-57MAKS: OK