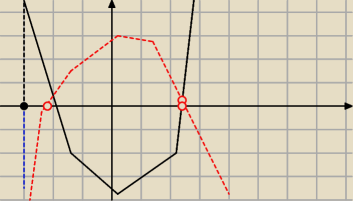
Dylemat Cy-57MAKS: Rozwazmy sytuacje ogolna mamy roznanie mx²+bx+c=0 mamy znalezc wartosc parametru m dla ktorego pierwiastki tego rowniania sa wieksze od zalozonej jakiejs liczby Sytuacja nr 1 m>0 parabola ramina w gore Niech ta liczba bedzie np (−3)

	−b
wiercholek paraboli		>−3
	2a

mf(−3)>0 Sytuacja nr2 (czerwona parabola m<0 ramiona w dol

	−b
Tez wierzcholek		>−3
	2a

Teraz wedlug mnie powinno byc mf(−3)<0 a w ksiazce mam mf(−3)>0

Jerzy: Cześć Masz trzy warunki: 1) Δ > 0 2) x_w > − 3 3) m*f(−3) > 0 bo, dla m < 0 , f(−3) < 0 , czyli m*f(−3) > 0 dla m > 0 , f(−3) > 0 , czyli m*f(−3) > 0

Adamm: pozostaje jeszcze przypadek m = 0

Cy-57MAKS: Dzien dobry Jerzy Nie moglem tego zalapac . Teraz juz wiem. Po prostu mnozymy liczbe ujemna przez ujemna dziekuje .

Jerzy: @Adamm , trzeci warunek eliminuje m = 0

Adamm: zauważ że podświadomie założyłeś m≠0

Adamm: podświadomie?... chyba złe słowo lepiej pasuje, pośrednio

Cy-57MAKS: Witam Adamm Nie mam nic wspomniane w rozwiazaniu o przypadku m=0 Wtedy mamy rownanie liniowe bx+c=0 bx=−c

	c
x= −
	b

I teraz to nasze wyliczone x musi byc w tym przypadku >(−3) ?

Adamm: tak, dla b≠0

Cy-57MAKS: Dziekuje .

Jerzy: W treści zadania jest napisane "pierwiastki" , a funkcja liniowa może mieć maksimum jeden.

Adamm: pierwiastki nie oznacza koniecznie dwa lub trzy lub więcej może to być w znaczeniu, jakiekolwiek pierwiastki jakie są a funkcja liniowa faktycznie może mieć więcej pierwiastków niż 1, w przypadku gdy jest tożsamościowo zerem

Jerzy: Racja, jeden lub nieskończenie wiele.