funkcja kwadratowa z parametrem wojtek.: 1. Wyznacz wszystkie wartości parametru m(m∊R), dla których równanie ¹₂x² − (m+1)x +m² + 3m + 2 = 0 ma dwa różne rozwiązania ujemne. 2. Wyznacz wszystkie wartości parametru m(m∊R), dla których dziedziną funkcji f(x)=√mx²+2(m−2)x+m−1 jest zbiór liczb rzeczywistych R. 3. Naszkicuj wykres funkcji f(x) = −x * |x − 2|. 4. Rozwiąż nierówność |x² − 9| ≤ 8x. 5. Naszkicuj wykres funkcji y = |x² − 2| x |−8|, a następnie, korzystając z tego wykresu, określ liczbę rozwiązań rowniania |x² − 2| x |−8| = m w zależności od wartości parametru m(m∊R). Bardzo proszę o rozwiązania krok po kroku! PLIISS

trygono: Opisz swój problem to Ci pomożemy, bo póki co napisałeś parę zadań i liczysz na gotowca?

Cy-57MAKS: Nr 1 Δ>0 x₁*x₂<0

ICSP: Rozwiązania mają być ujemne, więc ich iloczyn ma być ujemny ? Iloczyn dwóch liczb jest ujemny ? 1. Δ > 0 x₁ * x₂ > 0 − gwarantuje, że rozwiązania maja ten sam znak x₁ + x₂ < 0 −gwarantuje, że przynajmniej jedno rozwiązanie jest ujemne. To są warunki do pierwszego.

Cy-57MAKS: Ajj dwa rozne ujemne a nie jedno

wojtek.: moim problemem jest to, że tego totalnie nie ogarniam, muszę to zdać, a najlepiej mi się uczy właśnie na rozwiązanym przykładzie, więc tak. Liczę na gotowca

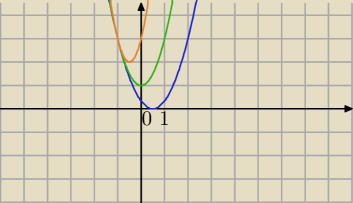
Mila: Zadanie2) Wyznacz wszystkie wartości parametru m(m∊R), dla których dziedziną funkcji f(x)=√mx²+2(m−2)x+m−1 jest zbiór liczb rzeczywistych R. 1) Wyrażenie pod pierwiastkiem może przyjmować tylko wartości nieujemne⇔ mx²+2(m−2)x+m−1≥0 dla każdego x∊R a) m>0 (wtedy mamy trójmian kwadratowy o wykresach tego typu co na rysunku) i Δ≤0 Δ=(2²*(m−2)²−4*(m−1)*m=4*(m²−4m+4)−4m²+4m=4m²−16m+16−4m²+4m Δ=−12m+16 −12m+16≤0⇔ −12m≤−16 /:(−12)

	16
m≥
	12

	4
m≥
	3

	4
Masz na rysunku wykresy funkcji pod pierwiastkiem dla m=		, m=2 i m=4
	3

Teraz analizuj, jak nie zrozumiesz to daj pytanie i dopiero potem możemy dalej pracować.