Rachunek wektorowy, iloczyn skalarny Dziadu: Wykazać że dla dowolnego trójkąta zachodzi związek s = ³₄d, gdzie s oznacza sumę kwadratów długości środkowych, zaś d sumę kwadratów długości boków trójkąta. Próbowałem na wektorkach coś działać ale nic ciekawego nie wyszło. Bardzo bym prosił o rozwiązanie analityczne

Saizou : Można zrobić tak, chociaż to nie będzie szybkie, tzn. niech A=(x_a, y_a), B=(x_b, y_b), C=(x_c, y_c) wówczas środek ciężkości trójkąta ABC wyraża się

	x1+x2+x3		y1+y2+y3
wzorem S=(		,		) oraz skorzystać z faktu, że środkowe
	3		3

przecinają się w stosunku 1:2.

Saizou : albo znaleźć wzór na długość środkowej zależnej od długości boków (lub go wyprowadzić) i zadanie staje się proste

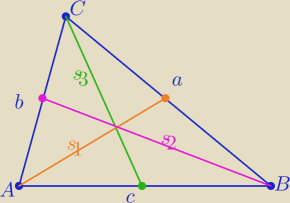
Eta: 4s₁²=2b²+2c²−a² 4s₂²=2a²+2c²−b² 4s₃²=2a²+2b²−c² + −−−−−−−−−−−−−−−−−−−−− 4(s₁²+s₂²+s₃²)=3(a²+b²+c²) 4s=3d

	3
s=		d
	4

c.n.w