Pole spoko, ale jak obwód? :-) marrro: W trójkącie ABC dane są: |BC|=a, |AB|=c, ∠ABC=β. Okrąg przechodzący przez punkty B i C przecina boki AB i AC w takich punktach D i E, że pole czworokąta BCDE stanowi 75% pola trójkąta ABC. Wyznaczyć obwód i pole czworokąta.

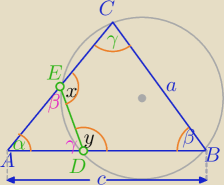
Mila: α+β+γ=180^o 1) czworokąt BCED wpisany w okrąg⇔ x+β=180^o i y+γ=180^o x=180−β i y=180−γ ∡AED=180−x=180−(180−β)=β ∡ADE=180−y=γ⇔ ΔADE∼ΔABC − oblicz skalę podobieństwa ============= Dalej poradzisz sobie ?

marrro: Jeśli EC=AC−c/2, a AC liczymy z tw. cosinusów oraz BD=c−AD i AD też z tw. cosinusów, to sobie poradziłem. Pytanie czy EC i BD, a wcześniej AC i AD można policzyć sprytniej, żeby nie wychodziły takie nieładne wyniki?

Mila:

	1
ΔADE∼ΔABC w skali k=
	2

	1
Obw. ΔADE=		obw.ΔABC
	2

Oblicz |AC|=b i wstaw do wzoru na obwód czworokąta

	1		1		1		3		1		1
Obw=a+c−		b+b−		c+		a=		a+		c+		b
	2		2		2		2		2		2

marrro: Ok, do policzenia obwodu, dzięki Twojemu pierwszemu wpisowi doszedłem. Moje poprzednie pytanie niepotrzebnie rozbudowałem Stosując Twój zapis powinno brzmieć prościej − czy b można sprytniej wyliczyć niż z twierdzenia cosinusów (bo to taki nieładny pierwiastek wychodzi)?

Mila: Wiem o co pytałeś wcześniej. Wczoraj i teraz nic prostszego nie przychodzi mi do głowy. (liczyłam też inaczej, ale to nie było prostsze)