równanie z parametrem
Nikto0: Proszę o pomoc przy zadaniach. Określ liczbe rozwiązań równania w zależności od parametru m,
jeśli a) |x−m|=3m−1 b)|5x−4|=|m+3|
1 lis 19:09
ite:
b)|5x−4|=|m+3|
1/ Naszkicuj wykres f(x)=|5x−4| .
2/ Określ ilość rozwiązań równania |5x−4|=k w zależności od wartości parametru k. Wpisz
je tutaj ← nie na kartce.
3/ Dalej trzeba będzie szukać rozwiązań równania k=|m+3| .
1 lis 20:27
ite:
a) |x−m|=3m−1
Można rozpatrywać dwa przypadki x−m≥0 i x−m<0.
Wtedy dla x≥m rówanie przyjmie postać x−m−3m+1=0
i dla x<m postać −x+m−3m+1=0 .
Jeśli rozwiązanie dla x≥m będzie większe od rozwiązania dla x<m, wyjściowe równanie będzie mieć
dwa rozwiązania. Gdy będą sobie równe, rozwiązanie będzie tylko jedno. W pozostałych
przypadkach rozwiązań nie będzie.
Wytłumaczyłam bardzo pobieżnie, jeśli coś jest niejasne, pytaj.
2 lis 10:40
Jerzy:
a)
Dla: 3m − 1 < 0 brak rozwiązań
Dla: 3m − 1 = 0 jedno
Dla: 3m − 1 > 0 dwa
2 lis 11:07
2 lis 11:09
Nikto0: mam błąd zeruje 4/5 a nie 5/4
2 lis 11:11
Jerzy:
b)
Dla m = −3 jedno rozwiązanie
Dla m ≠ −3 dwa
2 lis 11:27
Jerzy:
W której ty jesteś klasie ?
2 lis 11:32
Jerzy:
Jeśli już chcesz rysować ,choć nie ma takiej potrzeby,to:
Narysuj sobie wykres y = 5x − 4 i odbij to co jest pod osią OX nad oś.
2 lis 11:35
Nikto0: Jerzy jak to wyliczyłeś w 11:27? Ite nie rozumiem o co chodzi od tego fragmentu Jeśli
rozwiązanie dla x≥m będzie większe od rozwiązania dla x<m, wyjściowe równanie będzie mieć
dwa rozwiązania. Gdy będą sobie równe, rozwiązanie będzie tylko jedno. W pozostałych
przypadkach rozwiązań nie będzie.
2 lis 11:50
Nikto0: Nie jestem w żadnej klasie mam już skończone liceum.
2 lis 11:50
Jerzy:
|m + 3| = 0 ⇔ m = −3
|m + 3| > 0 ⇔ m ≠ −3
2 lis 11:57
Nikto0:
A tamto w 11:07?
2 lis 12:00
Jerzy:
Na podstawie definicji wartości bezwzględnej.
2 lis 12:02
Nikto0: I to w 11:07 kończy zadanie?
2 lis 12:05
Jerzy:
Tak,kończy,tylko trzeba obliczyć wartość m.
2 lis 12:08
Rumbarak : tak, ale nie dla Ciebie bo tego nie rozumiesz
na jednym ukladzie wspolrzednych narysuj sobie kilka wykresow funkcji y=|x−m| przyjmij sobie
np m=2 ,m=−3 ,m=1 m=−1
Zaobseruj jak uklada sie ten wykres .Zrob najpierw to
2 lis 12:17
Nikto0: będzie równe 1/3?
2 lis 12:18
Jerzy:
Skończyłaś liceum.A co teraz porabiasz ? Uczysz się nadal ?
2 lis 12:20
Nikto0: Ile będzie równe m? Na razie się tylko uczę.
2 lis 12:21
Jerzy:
12:17 , a w czym mają pomóc te wykresy w zrozumieniu rozwiązania tego zadania ?
2 lis 12:23
Jerzy:
A gdzie się uczysz ?
2 lis 12:23
Jerzy:
Masz problem z nierównością: 3m − 1 > 0 ?
2 lis 12:25
Nikto0: czyli m będzie się równało 1/3?
2 lis 12:26
Rumbarak :
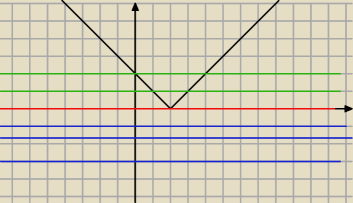
A w tym np ze zauwazy iz wykresy te maja jeden punkt wspolny z osia oX
Niezalenie od przyjetego m
czyli wykres funkcji y=3m−1 dla y=0 ma jeden punkt wspolny z wykresem y=|x−m|
| | 1 | |
Obliczamy 3m−1=0 stad m= |
| |
| | 3 | |
Nie bedzie punktow wspolnych dla y=3m−1<0 wylicz m
beda dwa punkty wspolne dla 3m−1>0 wylicz m
2 lis 12:34
Rumbarak : Na rysunku masz przykladowy wykres y=|x−2| czyli m=2
2 lis 12:37
Jerzy:
To pomaga.
2 lis 12:38
Jerzy:
12:26, podstaw i sprawdź.
2 lis 12:39
Jerzy:
Parametr m ma istotne znaczenie dla prawej strony równania w obu podpunktach i żadnego dla
lewej strony w podpunkcie a), więc po co podajesz przykład m = 2 ?
2 lis 12:43
Rumbarak : Jerzy odczep sie od dziecka
Podalem przykladowy wykres ,gdzie moze zrozumiec zadanie
Jesli Ty nie potrafiles wytlumaczyc to starlem sie to zrobic ja .
2 lis 12:49
Jerzy:
Tylko namieszałeś.
2 lis 12:50
Rumbarak : Przepraszam Jerzy
Uniosłem sie honorem
2 lis 14:08
Jerzy:
Nie ma sprawy.
2 lis 14:15
Nikto0: Dziękuję. Już rozumiem.
2 lis 14:19
