31 paź 21:37
52: A jakie jest polecenie?
31 paź 22:21
Rumbarak : A o co tak w ogole tutaj chodzi ?
Ani tresci ani polecenia . Wpisz tutaj tresc i polecenie
31 paź 22:21
Jerzy:
Ja widzę,że ty się dziecko starasz i dobrze, tylko przede wszystkim podaj treść zadania, a nie
zadawaj głupich pytań.
31 paź 22:41
1 lis 00:33
Rumbarak :
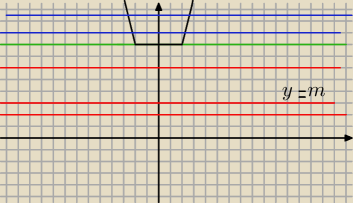
Nie ma waznego rysunku czy wykresu wiec tresc zadania mozna przepisac tutaj
Nie bedzie skakac sie co rusz po odnosniku
Zrob wykres tej funkcji y=|2x+4|+|2x−4| i tnij ten wykres prosta y=m i patrz gdzie jest
nieskonczenie wiele rozwiazan
Widac ze dla
m∊(−
∞.8) nie ma w ogole rozwiazan
m=8 jest nieskonczenie wiele rozwiazan
dla m∊(8,
∞) sa dwa rozwiazania .
1 lis 11:32
Nikto0: Nie wiem jak zrobić taki wykres.
1 lis 11:40
Rumbarak : y=|2x+4|+|2x−4|
rozpisujesz przedzialami i rysujesz wykresy funkcji w tych przedzialach
2x+4=0
x=−2
2x−4=0
x=2
masz przedzialy
1)x∊(−∞,−2)
2)x∊<−2,2)
3) x∊<2,∞)
1 lis 11:49
Nikto0: A tym sposobem z linku jak to zrobić?
1 lis 12:20
Rumbarak : jaki jest problem z narysowaniem tego wykresu ?
Rob sposobem ktory bardziej rozumiesz .Tutaj wydaje ten sposob z wykresem bo widac od razu
rozwiazanie .
1 lis 13:22
Nikto0: wykres wyszedł dobrze, ale chciałam znać też tamten sposób.
1 lis 13:27
Tomek : Nie bierzesz pod uwagę m=4x ponieważ m ma być parametrem czyli y=m jest funkcja stała a y=4x to
nie jest funkcja stała. Pamiętaj, ze jak parametr to m należy do zbioru liczb całkowitych
1 lis 16:07
Tomek : I jak już to m=4x
1 lis 16:08
Nikto0: Dziękuję
1 lis 16:09
Jerzy:
Nie pisz Tomku bzdur.Niby dlaczego parametr ma być całkowity ?
1 lis 17:15
Jerzy:
Aby wyjściowe równanie miało nieskończenie wiele rozwiązań,jego lewa strona musi być niezależna
od zmiennej x, czyli musi mieć stałą wartość,a tak jest dla x∊[−2,2].
1 lis 17:52
