Rozne
Rumbarak : Nr)
napisac rownanie krzywej bedacej zbiorem wszystkich punktow ,ktorych odleglosci od okregu o
rownaniu x
2+y
2=100i od punktu A(6,0) sa rowne
Naszkicuj ta krzywa
Nr2) Oblicz obwod tego z trapezow rownoramiennych majacych krotsza podsatwe 2a i ramie a
ktory ma najwieksze pole powierzchni
Nr3)
Wykazac ze jezeli rownanie x
3+ax+b ma pierwiastek podwojny to 4a
3+27b
2=0
Nr4)
| | cos2x | |
Rozwiazac nierownosc |
| <1 dla x∊(0,π) |
| | cosx | |
Nr5)
Wykazac ze okrag wpisany w trojkat prostokatny jest styczny do przeciwprostokatnej w punkcie
dzielacym przeciwprostokatna na dwa odcinki ktorych iloczyn dlugosci jest rowny polu
powierzchni tego trojkata
Nr6)
Z cyfr 1,2,3,4,5,6,7,8,9 losujemy bez zwracania trzy cyfry ukladajac je w kolejnosci losowania
w liczbe
Zakladajac ze wszystkie mozliwe do otrzymania w ten sposob liczby sa jednakowo prawdopodobne
,obliczyc prawdopodobienstwo otrzymania liczy mniejszej od 666.
Nr7)
W ostroslupie prawidlowym czworokatnym odleglosci srodka wysokosci od krawedzi bocznej i sciany
bocznej wynosza odpoweidnio a i b
Wyznaczyc objetosc ostroslupa i podac warunek rozwiazalnosci zadania .
Nr 8)
Wyznaczyc wartosci x dla ktorych istnieje granica
| | 1 | | 2x+1 | | (2x+1)n−1 | |
lim n→∞ [ |
| + |
| +...+ |
| ] |
| | x+2 | | (x+2)2 | | (x+2)n | |
Obliczyc ta granice
31 paź 00:19
Rumbarak : Probowalem nr 3
(x−m)2(x−c)= (x2−2xm+m2)(x−c)=
=x3−cx2−2mx2+2mcx+m2x−m2c=
x3+(−c−2m)x2+(2mc+m2)x−m2c
−c−2m=0
2mc+m2=a
−m2c=b
c=−2m
2m*(−2m)+m2=a
−3m2=a
−m2*(−2m)= 2m3=b
4*a3+27b2=4*(−27m6)+27*4m6=0
31 paź 00:42
Blee:
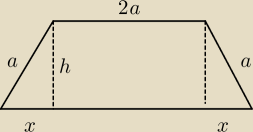
| | (4a+2x)*h | |
P = |
| = (2a+x)*√a2 − x2 |
| | 2 | |
| | 2ax+x2 | | −2x2 − 2ax + a2 | |
P'x = √a2−x2 − |
| = |
| |
| | √a2−x2 | | √a2−x2 | |
31 paź 01:17
Blee:
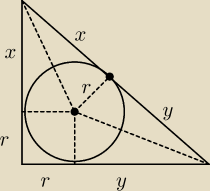
| | 1 | | 1 | |
Ptrójkąta = 2* |
| x*r + 2 |
| y*r + r2 = xr + yr + r2 |
| | 2 | | 2 | |
| | (x+r)(y+r) | |
xr + yr + r2 = |
| |
| | 2 | |
2xr + 2yr + 2r
2 = xy + rx + ry + r
2
xr + yr + r
2 = xy −> P
trójkąta = xy
31 paź 01:23
Blee:
Liczba mniejsza niż 666 to:
1) losujemy pierwszą cyfrę nie większą niż 5 (na 5 możliwości) −−− kolejne dowolne (więc mamy
8*7 możliwości)
co daje nam w sumie 5*8*7 możliwości
2) pierwszą cyfrę losujemy 6 (1 możliwość), drugą nie większą niż 5 (5 możliwości), trzecia
dowolna (7 możliwości)
co daje nam w sumie 1*5*7
| | 5*7*(1+8) | | 5 | |
P(A) = |
| = |
| |
| | 9*8*7 | | 8 | |
31 paź 01:25
Blee:
co do granicy ....
| | 2x+1 | | 2x + 4 − 3 | | 3 | |
q = |
| = |
| = 2 − |
| |
| | x+2 | | x+2 | | x+2 | |
| | 3 | |
|q| < 1 −> 1 < |
| < 3 −> −1 < x < 1 |
| | x+2 | |
dla takiego 'x' suma nieskończonego ciągu geometrycznego (czyli powyższa granica) będzie
skończona i nawet możesz ją obliczyć (masz wzór odpowiedni do tego)
31 paź 01:28
Blee:
A pozostałych dwóch mi się nie chce ruszać
31 paź 01:29
Rumbarak : dzieki Blee.
31 paź 08:36
Mila:
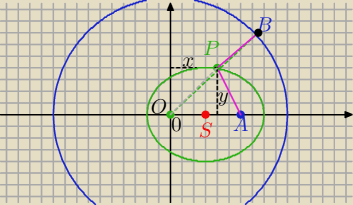
1) Napisać równanie krzywej będącej zbiorem wszystkich punktów ,których odległości od okręgu o
równaniu x
2+y
2=100 i od punktu A(6,0) są równe .
P=(x,y) ∊wnętrza okręgu
|OB|=R=10
|AP|=|BP|
|AP|=
√(x−6)2+y2
|PB|=10−|OP|=10−
√x2+y2
√(x−6)2+y2=10−
√x2+y2 obie strony nieujemne
x
2−12x+36=100−20
√x2+y2+x
2+y
2⇔
−64−12x=−20
√x2+y2 /: (−4)
| | 16 | |
3x+16=5√x2+y2 / 2 dla x≥− |
| |
| | 3 | |
9x
2+96x+256=25x
2+25y
2
16x
2−96x+25y
2−256=0
16*(x
2−6x)+25x
2=256
16*([(x−3)
2−9]+25y
2=256
16(x−3)
2+25y
2=400 /:400
| (x−3)2 | | y2 | |
| + |
| =1 elipsa o środku symetrii w punkcie S=(3,0) |
| 25 | | 16 | |
a=5, b=4
=======================
31 paź 18:14
Rumbarak : Dlaczego |AP|=|BP|?
31 paź 19:15
Mila:
Z treści zadania to wynika:
szukasz takich punktów, że:
"odległości od okręgu o równaniu x2+y2=100 i od punktu A(6,0) są równe "
31 paź 19:28
Rumbarak : Dzięki
31 paź 19:39
Mila:

31 paź 19:54
Rumbarak :

Zadanie nr 2
Obw= AB+2x+2a+2a= 2a+2x+4a= 6a+2x = 3a+x
x=a*cosβ
h=a*sinβ
P=(x+2a)*h
P=(a*cosβ+2a)*a*sinβ
P=a
2cos(β)*sin(β)+2a
2sin(β)
jak z tego obliczyc pochodna ?
31 paź 20:01
Rumbarak : P=a2sinβ(cosβ+2) po uporzadkowaniu
31 paź 20:19
Mila:
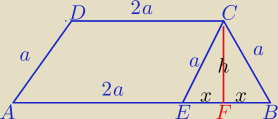
Zadanie 2.
a>0, x>0
1)
CE||AD
Ob=6a+2x
2) W ΔCFB:
h
2+x
2=a
2
h=
√a2−x2 , x>0 i x<a
P(x)=(2a+x)*
√a2−x2
P'(x)=(2a+x)' *
√a2−x2+(2a+x)*(
√a2−x2)'
| | (2a+x)*(−2x) | |
P'(x)=1*√a2−x2+ |
| = |
| | 2√a2−x2 | |
| | (2a+x)*(−x) | |
=√a2−x2+ |
| = |
| | √a2−x2 | |
P'(x)=0⇔
−2x
2−2ax+a
2=0
Δ=4a
2+4*2a
2=12a
2
| | 2a−2a√3 | | 2a+2a√3 | |
x1= |
| lub x2= |
| <0 |
| | −4 | | −4 | |
3)
obw=6a+a
√3−1
=================
31 paź 21:54
Rumbarak : Dzieki Mila
Jednak ponawiam pytanie . Jak policzyc z wpisu 20 : 19 pochodna .Tak jest we wskazowce i kaza
tez liczyc druga pochodna
31 paź 22:11
Mila:
Piszę

31 paź 23:17
Rumbarak : Dobrze

Nie spieszy sie az tak bardzo
31 paź 23:20
Mila:
Tam na końcu źle zapisałam wartość x, ( mąż mi zamontował nową klawiaturę i stąd kłopoty)
| | a*(√3−1) | |
obw=6a+2* |
| =5a+a√3 |
| | 2 | |
=========================
Pochodna:
P(β)=a
2cos(β)*sin(β)+2a
2sin(β)
P(β)=a
2(cosβ*sinβ+2sinβ)
P'(β)=a
2*[ (cosβ)'*sinβ+cosβ*(sinβ)'+2 (sinβ)']=
=a
2*[−sinβ*sinβ+cosβ*cosβ+2cosβ]=
=a
2*[−sin
2β+cos
2β+2cosβ]=a
2(*2cos
2β+2cosβ−1)
P'(β)=0⇔
2cos
2β+2cosβ−1=0
cosβ=t, cosβ>0
Δ=4+4*2=12
| | −2−2√3 | | −2+2√3 | |
cosβ= |
| <0 lub cosβ= |
| |
| | 4 | | 4 | |
===========
Druga pochodna:
P"(β)=(2cos
2β+2cosβ−1)=2*2cosβ*(−sinβ)+2*(−sinβ)]=
=−4cosβ*sinβ−2sinβ=
=−2sinβ*(cosβ+1) <0 dla ostrego kąta β
================================
Podoba mi się ten sposób.
31 paź 23:37
Rumbarak : Dziekuje Mila .
Bedzie co liczyc . Juz czas spac .
31 paź 23:44
Cy-57MAKS: Post 23 : 37
do czego tutaj byla potrzebna druga pochodna ?
3 lis 20:52
Cy-57MAKS: prosze o odpowiedz na moje pytanie .
3 lis 21:31
Adamm:
znak drugiej pochodnej decyduje czy mamy maksimum czy minimum
3 lis 21:34
Adamm:
Jeśli f'(x), f''(x), ..., f(n−1)(x) = 0, f(n)(x) ≠ 0
i n jest parzysta, to mamy maksimum jeśli f(n)(x)<0, i minimum w
przeciwnym wypadku
jeśli n jest nieparzysta, to ekstremum nie ma
3 lis 21:36
Cy-57MAKS: czyli jesli druga pochodna <0 to mamy max
jesli druga pochodna >0 to mamy min
dzieki
3 lis 21:37
Adamm:
ale ogólnie − ta metoda czasami działa, a czasami nie, więc lepiej uważać
3 lis 21:37
4 lis 14:12
Rumbarak: Bardzo ale to bardzo Ci dziekuje .
4 lis 14:17
ite: To było dla Cy−57MAKSa, sprostowanie do wpisu 21:37, ale dobrze jeśli się przyda.
4 lis 14:30
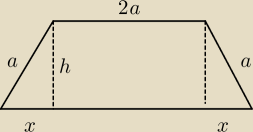

 1) Napisać równanie krzywej będącej zbiorem wszystkich punktów ,których odległości od okręgu o
równaniu x2+y2=100 i od punktu A(6,0) są równe .
P=(x,y) ∊wnętrza okręgu
|OB|=R=10
|AP|=|BP|
|AP|=√(x−6)2+y2
|PB|=10−|OP|=10−√x2+y2
√(x−6)2+y2=10−√x2+y2 obie strony nieujemne
x2−12x+36=100−20√x2+y2+x2+y2⇔
−64−12x=−20√x2+y2 /: (−4)
1) Napisać równanie krzywej będącej zbiorem wszystkich punktów ,których odległości od okręgu o
równaniu x2+y2=100 i od punktu A(6,0) są równe .
P=(x,y) ∊wnętrza okręgu
|OB|=R=10
|AP|=|BP|
|AP|=√(x−6)2+y2
|PB|=10−|OP|=10−√x2+y2
√(x−6)2+y2=10−√x2+y2 obie strony nieujemne
x2−12x+36=100−20√x2+y2+x2+y2⇔
−64−12x=−20√x2+y2 /: (−4)

 Zadanie nr 2
Obw= AB+2x+2a+2a= 2a+2x+4a= 6a+2x = 3a+x
Zadanie nr 2
Obw= AB+2x+2a+2a= 2a+2x+4a= 6a+2x = 3a+x
 Zadanie 2.
a>0, x>0
1)
CE||AD
Ob=6a+2x
2) W ΔCFB:
h2+x2=a2
h=√a2−x2 , x>0 i x<a
Zadanie 2.
a>0, x>0
1)
CE||AD
Ob=6a+2x
2) W ΔCFB:
h2+x2=a2
h=√a2−x2 , x>0 i x<a

 Nie spieszy sie az tak bardzo
Nie spieszy sie az tak bardzo