zadanie 1
bjkm: W trójkącie ABC poprowadzono dwusieczną CD. Wiadomo, że środek okręgu wpisanego
w trójkąt BCD pokrywa się ze środkiem okręgu opisanego na trójkącie ABC. Wyznacz miary kątów
trójkąta ABC
30 paź 17:32
BAI PING TING: tak tylko jest w trojkacie rownobocznym
30 paź 17:34
BAI PING TING: Przepraszam zle przeczytalem
Ślepne chyba juz

30 paź 17:40
Mila:
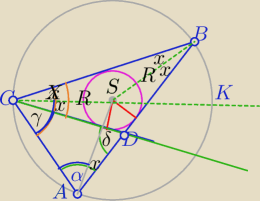
1) CD− dwusieczna kąta C
CK− dwusieczna kąta BCD
γ=2x
2) S leży na przecięciu dwusiecznych trójkąta BDC
|CS|=|BS|=R
3)
W równoramiennym ΔASC:
γ+x=α⇔2x+x=α
W ΔABC:
∡A+∡B+∡C=180
(3x+x)+(2x)+(2x+2x)=180
o
10x=180
o
x=18
o
|∡A|=4*18
o=72
o
|∡B|=2*18
o=36
o
|∡C|=72
o
===========
30 paź 19:23
Mila:
II sposób
30 paź 19:26
Eta:
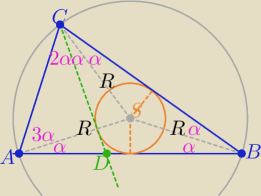
Rysunek powinien wyjaśnić wszystko

10α=180
o ⇒ α=18
o
Kąty trójkąta ABC maję miary
4α, 4α, 2α
72o, 72o, 36o
30 paź 19:32
Eta:
No to już
wyżej ... masz gotowca

30 paź 19:36

 1) CD− dwusieczna kąta C
CK− dwusieczna kąta BCD
γ=2x
2) S leży na przecięciu dwusiecznych trójkąta BDC
|CS|=|BS|=R
3)
W równoramiennym ΔASC:
γ+x=α⇔2x+x=α
W ΔABC:
∡A+∡B+∡C=180
(3x+x)+(2x)+(2x+2x)=180o
10x=180o
x=18o
|∡A|=4*18o=72o
|∡B|=2*18o=36o
|∡C|=72o
===========
1) CD− dwusieczna kąta C
CK− dwusieczna kąta BCD
γ=2x
2) S leży na przecięciu dwusiecznych trójkąta BDC
|CS|=|BS|=R
3)
W równoramiennym ΔASC:
γ+x=α⇔2x+x=α
W ΔABC:
∡A+∡B+∡C=180
(3x+x)+(2x)+(2x+2x)=180o
10x=180o
x=18o
|∡A|=4*18o=72o
|∡B|=2*18o=36o
|∡C|=72o
===========
 Rysunek powinien wyjaśnić wszystko
Rysunek powinien wyjaśnić wszystko  10α=180o ⇒ α=18o
Kąty trójkąta ABC maję miary
4α, 4α, 2α
72o, 72o, 36o
10α=180o ⇒ α=18o
Kąty trójkąta ABC maję miary
4α, 4α, 2α
72o, 72o, 36o
