Równoważność Nadine: Niech A={a,b,c,d}. Znajdź najmniejszą relację równoważności R⊆A×A taką, że (a,c)∈R i (a,d)∈R. Siedzę nad tym już tydzień i nie potrafię nic zrozumieć. Nie proszę o nauczenie ale o zrobienie z pokrótkim wytłumazceniem ponieważ potrzebuję tego na już, a ogarnę jutro na korkach.

Pan Kalafior: skoro jest to relacja równoważności, to ze zwrotności (a, a), (b, b), (c, c), (d, d)∊R Skoro (a, c)∊R to (c, a)∊R, i skoro (a, d)∊R to (d, a)∊R. Ponieważ (a, d)∊R i (c, a)∊R, to (c, d)∊R, skąd (d, c)∊R. Zatem {(a, a), (b, b), (c, c), (d, d), (a, c), (c, a), (a, d), (d, a), (c, d), (d, c)}⊆R, ale to relacja równoważności zawierająca (a, c) oraz (a, d), zatem {(a, a), (b, b), (c, c), (d, d), (a, c), (c, a), (a, d), (d, a), (c, d), (d, c)}=R. Łatwiej jedynie scharakteryzować R poprzez jej klasy abstrakcji. Z (a, c)∊R, (a, d)∊R wiemy że c, d∊[a]_R. Stąd R musi być relacją równoważności o klasach abstrakcji {a, c, d} i {b}.

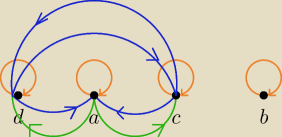
ite: Zilustruję ten wykład: (a, c), (a, d) te pary były dane (a, a), (b, b), (c, c), (d, d) pary dodane ze względu na zwrotność (c, a), (d, a), (c, d), (d, c) pary dodane ze względu na symetryczność i przechodniość I widać, że a,c,d należą do tej samej klasy abstrakcji, b do niej nie należy.

Pan Kalafior: Piękna ilustracja