Liczby zespolone, moduły
cdc: Liczby zespolone (moduły)
Zaznacz na płaszczyźnie zbiór A:
a) I iz+2 I= I iz−2 I (powinno wyjść prosta y=x)
b) I −2z I= I 4z−4 I (powinno wyjść okrąg o środku (4/3,0) r=2/3)
Bardzo proszę o rozwiązanie i wytłumaczenie w miarę możliwości. Z góry dziękuję

28 paź 17:16
cdc: Przykład a powinien wyglądać tak: I iz+2 I= I iz−2i I
28 paź 17:18
Mila:
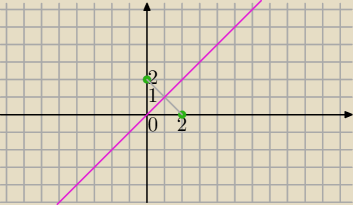
a) |iz+2|=|iz−2i|⇔najpierw przekształcamy
|iz−2i
2|=|i|*|z−2|
|i|*|z−2i|=|z−2|
|z−2i|=|z−2| zbiorem punktów jest symetralna odcinka o końcach:
(0,2), (2,0))
y=x
b)
dobrze przepisane?
|−2z|=|4z−4|
28 paź 18:54
cdc: Dziękuję. Tak, drugi przykład jest dobrze przepisany
29 paź 09:10
Mila:
b)
|z|=|2z−2|⇔
|z|=2*|z−1|
z=x+iy, gdzie x,y∊R
|x+iy|=2*|x+iy−1|
√x2+y2=2*
√(x−1)2+y2 /
2
x
2+y
2=4*(x
2−2x+1+y
2)
x
2+y
2=4x
2−8x+4+4y
2
3x
2−8x+4+3y
2=0 /:3
| | 8 | | 4 | |
(x2− |
| x)+ |
| +y2=0 uzupełniam do kwadratu dwumianu: |
| | 3 | | 3 | |
| | 4 | | 16 | | 4 | |
(x− |
| )2− |
| + |
| +y2=0 |
| | 3 | | 9 | | 3 | |
| | 4 | | 2 | |
okrąg: S=( |
| ,0), r= |
| |
| | 3 | | 3 | |
==================
29 paź 16:55

 a) |iz+2|=|iz−2i|⇔najpierw przekształcamy
|iz−2i2|=|i|*|z−2|
|i|*|z−2i|=|z−2|
|z−2i|=|z−2| zbiorem punktów jest symetralna odcinka o końcach:
(0,2), (2,0))
y=x
b)
dobrze przepisane?
|−2z|=|4z−4|
a) |iz+2|=|iz−2i|⇔najpierw przekształcamy
|iz−2i2|=|i|*|z−2|
|i|*|z−2i|=|z−2|
|z−2i|=|z−2| zbiorem punktów jest symetralna odcinka o końcach:
(0,2), (2,0))
y=x
b)
dobrze przepisane?
|−2z|=|4z−4|