RELACJA BIANRNA bluee: Wykazać, że relacja binarna ~ na płaszczyźnie R² zdefiniowana za pomocą formuły: (a,b)~(x,y) ⇒∃λ∊R*: x=λa y=λb jest relacją równoważności. Opisać klasy abstrakcji [(0,0)]_~ oraz [(1,−2)]_~.

bluee: Nie wiem jak udowodnić, że relacja jest symetryczna?

jc:

	1
(a,b) ~ (x,y)⇒ (x,y)=k(a,b) dla pewnego k≠0 ⇒ (a,b)=		(x,y) ⇒ (x,y) ~ (a,b)
	k

Klasy abstrakcji [(0,0)] = {(0,0)} [(1,−2)] = {(k,−2k): k∊R, k≠0} Pomijając (0,0), klasy abstrakcji to kierunki na płaszczyźnie.

bluee: Niech t∊R*. Opisać klasy abstrakcji [(0,t)]_~,[(t,t)]_~, oraz [(t,−t)]_~, gdzie ~ to relacja z poprzedniego zadania. Jaka jest interpretacja geometryczna relacji ~? (Inaczej mówiąc, co zaznaczy z geometrycznego punktu widzenie, że dwa punkty są w tej relacji) Opisać − w języku geometrii − iloraz R²/~. [(0,t)]_~= {x=0,y=tλ} [(t,t)]_~={x=tλ,y=tλ} [{t,−t}]_~={x=tλ,y=−tλ} Oznacza to, że punkt (a,b) został przeniesiony o wektor o współrzędnych [λ,λ] tworząc punkt (x,y). Iloraz R²/~ to przestrzeń pozbawiona punktów o współrzędnych odpowiadającym relacji ~. TAK TO ROZWIĄZAŁAM. NIE MAM ODPOWIEDZI, ALE WYDAJE MI SIĘ, ŻE CO JEST ŹLE. MÓGŁBY MNIE KTOŚ POPRAWIĆ?

bluee: Gdyby to było przesunięcie o wektor to było by x=λ+a... Czy można tą parę uporządkowaną jako współrzędne wektora, a nie punktu?

jc: Klasą abstrakcji (a,b)≠(0,0) jest prosta przechodząca przez (0,0) i (a,b), ale bez punktu (0,0). Klasą abstrakcji (0,0) jest zbiór {(0,0)}.

bluee: Czy k i λ to dla Ciebie to samo? Dlaczego wprowadziłeś kolejną zmienną?

bluee: Czyli można powiedzieć, że punkty będące w relacji ~ leżą na prostych przechodzących przez punkt (0,0) oraz przez punkt (x,y)? Czyli Iloraz R²/~ to zbiór wszystkich prostych nieprzechodzących przez punkt (0,0) ?

ite: Jaki zbiór oznaczyłaś przez R* ?

bluee: Nie wiem , tak było w poleceniu.

ite: Czyli λ może być równe 0 ?

Pan Kalafior: @ite R^* = R\{0}

ite: Nie wiedziałam, dzięki.

Pan Kalafior: Zazwyczaj oznacza się tak przy pierścieniach

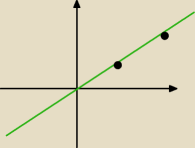
jc: Dwa punkty (a,b) i (x,y) różne od (0,0) są w relacji ⇔ punkty (a,b), (x,y), (0,0) są współliniowe.

bluee: R²/~ to będzie punkt (0,0)

Pan Kalafior: R²/∼ składa się z prostych przechodzących przez punkt (0, 0), bez zera, oraz zbioru {(0, 0)}

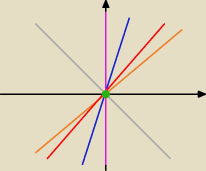
ite: bluee tutaj widać, że ta relacja ma nieskończenie wiele nieskończonych klas abstrakcji (i jedną jednoelementową), które "wypełniają" płaszczyznę. np. klasy równoważności z 17:15 [(0,t)]_~ [(t,t)]_~ [t,−t]_~ [t,2t]_~ [0,0]_~={(0,0)}

bluee: ite zgadzam się Tobą. Wydaje mi się, że będzie to pusta przestrzeń → R²/~ to poprostu zbiór pusty, Właściwie taki był mój pierwszy pomysł. Ale wydawało mi się to zbyt proste.

jc: Dlaczego R²/~ miałby być zbiorem pustym? Przecież to zbiór klas abstrakcji. Relacja równoważności w niepustym zbiorze ma co najmniej jedną klasę abstrakcji.

ite: bluee źle rozumiesz pojęcie zbioru ilorazowego. Jest dokładnie odwrotnie niż piszesz o 17:15.

bluee: Czyli iloraz to zbiór R² ?

bluee: Czyli to nie jest różnica?

jc: O jakiej różnicy piszesz? Zbiór / relacja = zbiór klas abstrakcji

bluee: Możesz napisać dwa słowa więcej. Dla mnie A/B oznacza, to co jest w i czego nie ma w B.

bluee: OK, wygłupiłam już wiem o co chodzi.

jc: A−B, ewentualnie A\B (tego zapisu nie lubię). A/B to iloraz, nie różnica.