zaznacz na płaszczyźnie zbiory Nikto0: Witam. Nie rozumiem tego zadania https://zadania.info/d714/3792561 nie widzę tego ograniczenia <−1,5> A w tym zadaniu https://zapodaj.net/34ab5251e9c19.jpg.html mogę zrobić podobnie jak to https://zapodaj.net/6bc7220ef0b32.jpg.html Kolejne pytanie czy mogę zrobić tak https://zapodaj.net/cdfae427a0104.jpg.html

abcd : Tyle razy zwracano ci uwage Mozesz obracac te rysunki? Pierwsze dlaczego nie widzisz tego ograniczenia To co pod pierwiastkiem musi byc ≥0

Nikto0: A w tym zadaniu https://zapodaj.net/b1981644c94ff.jpg.html mogę zrobić podobnie jak to https://zapodaj.net/441d946e447e0.jpg.html Kolejne pytanie czy mogę zrobić tak https://zapodaj.net/d6e18b58773aa.jpg.html Tak ale nie widzę tego ograniczenia na rysunku

Nikto0: Przepraszam, ale nie umiem obracać zdjęć na komórce będę korzystała z komputera.

Jerzy: Rozpatrujesz 4 przypadki: x ≥ 0 i y ≥ 0 , wtedy masz: x + y ≤ 4 ⇔ y ≤ −x + 4 x ≥ 0 i y < 0 , wtedy masz x − y ≤ 4 ⇔ y ≥ x − 4 Rozpisuj pozostałe dwa przypadki.

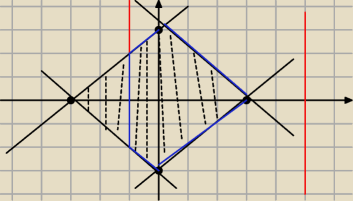
abcd : Po rozwiazaniu nierownosci x²−4x−5≤0 masz ograniczenie co do x_ow czyli x∊<−1,5> zostaje ci taka nierownosc |x|+|y|−3≤0 Zapisujesz ja w postaci |y|≤−|x|+3 Teraz 4 przypadki 1) y≥0 i x≥0 nierownosc ma postac y≤−x−3 rysujesz prosta y=−x−3 i zaznaczasz w 1 cwiartce to co pod wykresem razem z prosta 2) y≥0 i x<0 nierownisc ma postac y≤−(−x)+3 to y≤x+3 rysujewsz prosta y=x+3 i w 2 cwiartce (bo tam masz y≥0 i x<0 zaznaczasz to co pod wykresm razem z prosta 3) y<0 i x≥0 nierownosc ma postac −y≤−x+3 to y≥x−3 robisz to samo 4) y<0 i x<0 masz nierownosc −y≤−(−x)+3 −y≤x+3 to y≥−x−3 Rysujesz i zaznaczas Na poczatku mialas ograniczenie co do x ∊<−1,5> na osi OX zaznaczasz to ograniczenie To co na niebiesko to zbior A

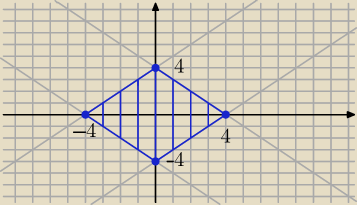
ICSP: |x| + |y| ≤ a Opisuje kwadrat o wierzchołkach (0 ,a) , (a , 0) , (0 , −a) , (−a , 0) Oczywiście wymagane jest tutaj założenie a > 0

Jerzy: A skąd takie załozenie ?

Nikto0: Jerzy x<0 i y≥0 −x+y≤4 y≤4+x x<0 i y<0 −x−y≤4 −y≤4+x y≥−x−4

Jerzy: Masz wszystko. Teraz rysuj każdy przypadek pamiętająć o założeniach dla każdego z nich.

Nikto0: Nie wiem jak to rozrysować.

Jerzy:

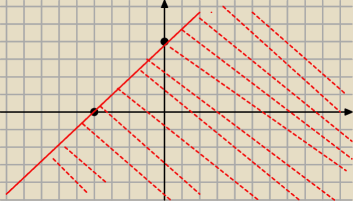
abcd : Rozpisz jeszcze pozostale dwa przypadki Teraz np y≤4+x wraz z prosta Rozrysuj pozostale przypadki i zobacz gdzie bedzie czesc wspolna rozwiazan

Nikto0: wyliczyłam do tego momentu https://zapodaj.net/eb47ae97c12dc.jpg.html jak obliczyć co się stanie z tym gdy podstawię do jakiegoś wzoru funkcji x=0

Nikto0: dlaczego x=0 i y=−4 w 10:59

Jerzy: Rysujesz 4 proste: y = x + 4 y = −x + 4 i zakreslasz wszystko pod nimi y = x − 4 y = −x − 4 i zakreślasz wszystko co jest nad nimi Na końcu część wspólna , czyli wnetrze kwadratu z jeko obrzeżem

Nikto0: Dziękuję Jerzy, abcd