trokat rownoramienny
abcd:
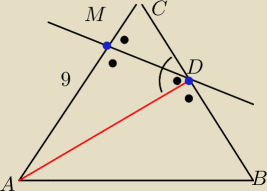
W trojkacie rownoramiennym o podstawie AB= 5
√10poprowadzono wysokosc AD do ramienia BC
Z punktu D poprowadzono prostopadla do AC przecinajaca AC w punkcie M .
AM=9 . Oblicz ramie trojkata
23 paź 13:58
abcd: Nikt nie chce pomoc?

23 paź 15:20
piotr: czy to cała treść?
23 paź 16:03
abcd: Tak cala i ma byc
w trojkacie rownoramiennym ABC
23 paź 16:06
abcd: Odpowiedz jest taka
Rownanie 9x
3−250x
2+125
2=0
| | 25 | |
Dlugosc 25 lub |
| (1+√37) |
| | 18 | |
23 paź 16:26
Mila:
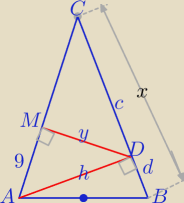
|AB|=5
√10,|AC|=|BC|=x,
|MC|=x−9, x>9
c+d=x
1) W ΔADC: y
2=9*(x−9)=9x−81
2) ΔCMD:
c
2=y
2+(x−9)
2⇔c
2=9x−81+x
2−18x+81
c2=x2−9x
3) ΔAMD:
h
2=y
2+9
2⇔h
2=9x−81+81
h2=9x
4) ΔADB:
(5
√10)
2=h
2+d
2
250=9x+d
2
5)
c+d=x /
2
c
2+2cd+d
2=x
2
x
2−9x+250−9x+2
√(x2−9x)*(250−9x)=x
2
250−18x+2
√(x2−9x)*(250−9x)=0
125−9x+
√(x2−9x)*(250−9x)=0
√(x2−9x)*(250−9x)=9x−125 /
2 ,9x>125
250x
2−9x
3−2250x+81x
2=81x
2−2250x+125
2
−9x
3+250x
2−125
2=0
9x3−250x2+1252=0
Dalej sam
23 paź 19:17
abcd: Dziekuje Mila
W sumie duzo liczenia nie bedzie
bo +/−1 +/−5 +/−25 / +/−125
23 paź 19:26
Mila:
Właściwie tylko sprawdzasz x=25 − patrz ograniczenia. Potem dzielenie i równanie kwadratowe.
23 paź 20:23
efgh: to proste jak p..
23 paź 21:10
abcd: Wyszlo mi jak w odpowiedzi
Post wyzej jest bardziej obrazliwy niz moj w tamtym poscie
23 paź 21:23
Mila:
No to urywajcie sobie głowy. Dobranoc

23 paź 22:05
abcd: Dobrej nocy

23 paź 22:14
 W trojkacie rownoramiennym o podstawie AB= 5√10poprowadzono wysokosc AD do ramienia BC
Z punktu D poprowadzono prostopadla do AC przecinajaca AC w punkcie M .
AM=9 . Oblicz ramie trojkata
W trojkacie rownoramiennym o podstawie AB= 5√10poprowadzono wysokosc AD do ramienia BC
Z punktu D poprowadzono prostopadla do AC przecinajaca AC w punkcie M .
AM=9 . Oblicz ramie trojkata

 |AB|=5√10,|AC|=|BC|=x,
|MC|=x−9, x>9
c+d=x
1) W ΔADC: y2=9*(x−9)=9x−81
2) ΔCMD:
c2=y2+(x−9)2⇔c2=9x−81+x2−18x+81
c2=x2−9x
3) ΔAMD:
h2=y2+92⇔h2=9x−81+81
h2=9x
4) ΔADB:
(5√10)2=h2+d2
250=9x+d2
|AB|=5√10,|AC|=|BC|=x,
|MC|=x−9, x>9
c+d=x
1) W ΔADC: y2=9*(x−9)=9x−81
2) ΔCMD:
c2=y2+(x−9)2⇔c2=9x−81+x2−18x+81
c2=x2−9x
3) ΔAMD:
h2=y2+92⇔h2=9x−81+81
h2=9x
4) ΔADB:
(5√10)2=h2+d2
250=9x+d2

