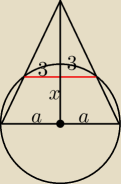
Trojkat rownoramienny abcd: W trojkacie rownoramiennym wysokosc wynosi 10 Okrag ktorego srednica jest podstawa trojkata przecina ramiona trojkata w punktach M i N MN=6 Oblicz przynajmniej jedna z mozliwych dlugosci podstawy trojkata . Chyba dobry zrobilem rysunek do zadania

10		10−x
	=
a		3

30=10a−ax a(10−x)=30

	30
a=		i x<10
	10−x

Dlugosc podstawy mozliwa

	30
2a=2/div>
	10−x

abcd: Natomiast w odpowiedzi jest tak Dlugosc podstawy 2x spelnia warunek 6<2x<20 Na x otrzymujemy rownanie x⁴−109x²+600x−900=0 . Wiec co zrobilem zle

abcd:

abcd: jest ktos w stanie wytlumaczyc jak zrobic to zadanie ?

V: rysunek niezły ale brakuje oznaczeń, niech ΔABC gdzie C − górny wierzchołek, dodatkowo pkt. D−przeciecie się wysokości z czerwoną kreską wtedy x² + 10² = AC²

3		CD		MC
	−		=
x		10		AC

MC² = 3³ + CD² rozwiąż

abcd: Dziekuje . Dokocze potem .jestem juz zmeczony Robilem go zanim spojrzalem do odpowiedzi Pytanie Dlaczego u mnie 2a musi byc <20 bo dlaczego >6 to rozumiem .

V: z Talesa