Liczby zespolone ballin: Naszkicować zbiór wszystkich liczb zespolonych z dla których a) liczba v jest rzeczywista b) liczba v jest czysto urojona

	z
v=
	iz+4

Proszę o pomoc i wytłumaczenie jak obliczyć zadanie tego typu. Ps W książce w odpowiedziach jest założenie że z≠4i to błąd czy tak powinno być, ponieważ moim

	4
zdaniem powinno być z≠		?
	i

Jerzy:

	4
z ≠ 4i ⇔ z ≠
	i

x + iy		x + iy		x +iy
	=		=
i(x + iy) + 4		xi − y +4		(4 − y) +ix

Teraz wymnazasz licznik i mianownik przez sprzężenie mianownika. Dalej: a) część urojona = 0 b) część rzeczywista = 0

PW: W książce jest poprawnie. Dla z=4i w mianowniku mamy i(4i) + 4 = −i²•4 + 4 = − 4 + 4 = 0. Rozwiązanie: liczba v jest rzeczywista, gdy

	z
		= r, r∊R.
	iz+4

z = (iz + 4)r z − irz = 4r z(1 − ir) = 4r

	4r
z =
	1 − ir

	4r(1+ ri)
z =
	(1 − ir)(1 + ir)

	4r(1 + ri)
z =
	12 − (ir)2

	4r(1 + ri)
z =		.
	1 + r2

PW: Poprawka: w drugim wierszu miało być i(4i) + 4 = i²•4 + 4 = −4 + 4 = 0

Jerzy: Pierwsza linijka , to oczywiscie pomyłka. Załozenie:

	−4		−4i		−4i
iz + 4 ≠ 0 ⇔ iz ≠ − 4 ⇔ z ≠		⇔ z ≠		⇔ z ≠		⇔ z ≠ 4i
	i		i2		−1

ballin: Dziękuje za pomoc, jednak cały czas nie rozumiem skąd bierze się to z≠4i. Czy mógłbym prosić o wytłumaczenie jeszcze tego ?

ballin: Dziękuje bardzo

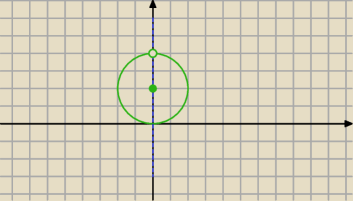
Jerzy: Rozwiązanie: a) zielony okrąg S(0,2) r = 2 b) prosta x = 0 , bez punktu (0,4)

jc: Zbiór liczb Re z = 0 jest prostą, podobnie ze zbiorem Im z =0. Funkcja homograficzna Przekształca okręgi i proste w okręgi i proste. Funkcja odwrotna do homgraficznej jest funkcją homograficzną.

	2z+3
Np. zbiór Im(		) = 0 jest okręgiem.
	5z+7