nierówności kwadratowe Paweł: Rozwiąż nierówności: a) x² − 5x + 6<0 b) x² − 6x + 10>0 c) x² + 2x + 2≤0 d) 2x² + 5x − 3<0 e) 6x² − x − 2≤0 f) (3−2x)(x+5)≤0 g) (x−3)(x−5) ≤0 h) (2x−1)(x+4)>0 Ja rozwiązuje je tak: (x w rozwiązaniu oznacza mnożenie) np. a) x² − 5x + 6<0 Δ = b² − 4ac Δ(−5)² − 4x1x6=25−24=1⇒√1 = 1

	−b − √Δ		5−1		4
x1 =		=		=		= 2
	2a		2		2

	−b + √Δ		5+1		6
x2 =		=		=		= 3
	2a		2		2

i z narysowaniem na osi mam już problem proszę o szybką pomoc

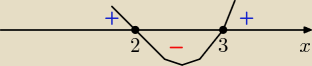Eta: a) x²−5x+6<0 => ( x −2)(x−3)<0 ramiona paraboli do góry wybierasz wartości ujemne ( z pod osi OX bez miejsc zerowych bo nierówność <0 odp: x€( 2,3) pozostałe podobnie ( narysuj szkic paraboli , pamiętaj jak są skierowane ramiona jezeli masz nierówność np; ≥0 to wybierasz wartości z nad osi OX wraz z miejscami zerowymi czyli otrzymujesz przedział obustronnie domknięty powodzenia

Eta: zobacz tu ( zadania)https://matematykaszkolna.pl/strona/93.html

aneczka: zaznaczasz na osi miejsca zerowe (2,3), rysujesz parabolę− ramiona do góry masz zaznaczyć mniejsze od zera (czyli pod osią to co się znajduje jest to przedział: xe: (2;3) Ps To ma być parabola (narysowałam tak, bo tutaj nie wiem jak parabole zrobić , ale wiesz o co chodzi )

Paweł: a jeżeli delta wyszła ujemna to co mam zrobić?

Eta: to wtedy , jeżeli parabola ramionami do góry , to cała jest nad osią czyli osiaga tylko wrtości >0 a jeżeli ramionami do dołu , cała leży pod osią oX , czyli osiaga tylko wartości ujemne

Paweł: ok dzięki za pomoc... jesteście wielkie jeszcze raz dzięki

Eta:

jmg: