średnice trapezu
kamil:
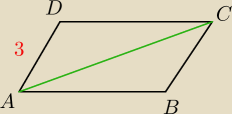
kąt DAC = 45
kąt ACD = 30
|AD|=3
Czworokąt na rysunku jest równoległobokiem
Oblicz |AC|
2+|BD|
2
Potrzebuję pomocy bo nie mam pojęcia jak to obliczyć
21 paź 00:09
Maciess:
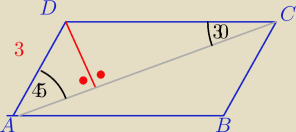
Miałeś twierdzenie cosinusów?
21 paź 00:34
Robert: tak ale nie wiem jak to wyliczyć tym sposobem, liczyłem ze |AC|=(3*√2)/2+(3*p{6|)/2
bo sin45=h/3 =>h=3*√2/2 (pierwsza część średnicy, a tg30=h/x => x=3*√6/2 ale nie wiem co z
drugą średnića
21 paź 00:43
Maciess:
∡ADC=105o
∡DCB=75o
z trójkątów ekierek mamy |DC|=|AB|=3√2
|AC|2=32+(3√2)2−2*3*3√2cos(105o)
|BD|2=32+(3√2)2−2*3*3√2cos(75o)
dodajemy stronami
|AC|2+|BD|2=54−18√2(cos(105o)+cos(75o))
|AC|2+|BD|2=54−18√2(2*cos(90o)*cos(15o))
|AC|2+|BD|2=54−18√2(2*0*cos(30o))=54
o ile czegoś nie skopałem bo godzina juz nie ta
21 paź 00:59
Mila:
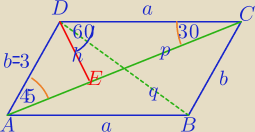
|AC|=p, |DB|=q
1)
ΔAED− Δprostokątny równoramienny
W ΔDEC: a=3
√2
2) W dowolnym równoległoboku o bokach a, b:
p
2+q
2=2a
2+2b
2 ( z tw. cosinusów)
3)
p
2+q
2=2*3
2+2*(3
√2)
2
p
2+q
2=54
=======
21 paź 16:06
 kąt DAC = 45
kąt ACD = 30
|AD|=3
Czworokąt na rysunku jest równoległobokiem
Oblicz |AC|2+|BD|2
Potrzebuję pomocy bo nie mam pojęcia jak to obliczyć
kąt DAC = 45
kąt ACD = 30
|AD|=3
Czworokąt na rysunku jest równoległobokiem
Oblicz |AC|2+|BD|2
Potrzebuję pomocy bo nie mam pojęcia jak to obliczyć
 Miałeś twierdzenie cosinusów?
Miałeś twierdzenie cosinusów?
 |AC|=p, |DB|=q
1)
ΔAED− Δprostokątny równoramienny
|AC|=p, |DB|=q
1)
ΔAED− Δprostokątny równoramienny