Wielomian Pilnee: Wykaż że wielomian W(x)=10ax⁴−4ax³+a²x²+6x−2 ma w orzedziale <0;1> pierwiastek rzeczywisty dla każdej wartości a. Twierdzenie o zerowaniu funkcji

Blee: A niby takiego 'pilnego' jest o 22:30 że mamy lecieć i Ci gotowca dawać

Saizou : Twoerdzenie Darboux zastosuj

ABC: ponadto twierdzeń o zerowaniu jest kilka podaj dokładnie z którego masz skorzystać

Mariusz: W(0)=−2 W(1)=10a−4a+a²+6−2 a²+6a+4=(a+3)²−5 (a+3−√5)(a+3+√5) Wyróżnik trójmianu jest dodatni więc nie wiem jak to twierdzenie mogłoby pomóc Dla a ∊ (−∞,−3−√5)∪(−3+√5,∞) to twierdzenie mogłoby pomóc ale nie dla każdego a

Mariusz: ABC jakiego twierdzenia proponowałbyś użyć bo sugerowane przez Saizou twierdzenie Darboux nie zadziała dla każdego a

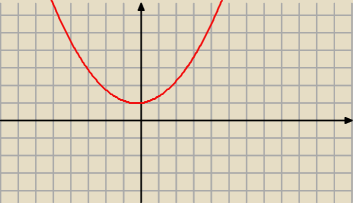
ABC: jeśli się nie pomyliłem w rachunkach to jest to sztuczka z zamaskowaniem jednego końca przedziału: W(1/2)=10/16*a−4/8*a+1/4*a²+3−2=1/4a²+1/8a+1 i teraz zadziała

Mariusz: Byłoby bardziej widoczne gdybyś zapisał ten trójmian w postaci kanonicznej

	1		1		63
=		(a+		)2+
	4		4		64

Całkiem niezły pomysł z tym zawężeniem przedziału

ABC: wczułem się w tego co układał zadanie że pewnie powiększył przedział dla zmyłki