Zbiór wartości funkcji trygonometrycznej Forrest: Witam, mógłby mi ktoś rozrysować rysunek pomocniczy do zadania poniżej, ponieważ wiesz jakie jest rozwiązanie tzn. trzeba wyznaczyc q − najmniejsza wartość i później sprawdza g(−1) i g(1) ale nie potrafie zrozumieć jak to działa, dlatego chciałbym to na wykresie zobaczyć. Oblicz zbiór wartości funcji: 4sin²αx − 4sinx + 5 Zw = <4; 13>

ABC: ile wynosi α?

Forrest: Literówka, przepraszam, bez a, samo 4sin²x

ABC: możesz to tak zapisać (2sinx−1)²+4 teraz rozumiesz czemu taki zbiór wartości?

Forrest: Ten zapis rozumiem , natomiast próbuję zrozumieć ten drugi sposób z f.kwadratową czyli gdzie 4t²−4t + 5 , t = sinx

Forrest: Chyba, że na tym to polega, żeby to zapisywać w postaci kanonicznej, ale chciałbym to graficznie zobaczyc i zrozumieć

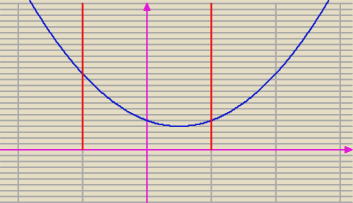
ABC: to polega na tym że szukasz największej i najmniejszej wartości funkcji kwadratowej na przedziale <−1,1> bo takie wartości przyjmuje sinus argumentu rzeczywistego

Forrest: Dzięki za rysunek, zrozumiałem. Czyli gdyby a<0 f.kwadratowej to q było by wartością max natomiast któryś z punktów granicznych f(1) lub f(−1) najmniejszą wartością

ABC: to zależy jeszcze od tego czy wierzchołek by się łapał w tym przedziale, jeśli nie to na końcach byłyby te wartości