fgdf Jarosław Koczyński:

	2+2i
Im(		) = 1
	z

Zaznaczyć w płaszczyźnie

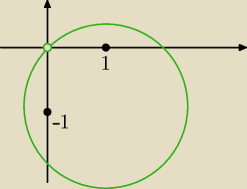
ite: o to wynik

Mila: z≠0 z=x+iy, gdzie x,y∊R

	2+2i		(2+2i)*(x−iy)
v=		=		=
	x+iy		x2+y2

	2x−2iy+2ix−2i2y		(2x+2y)+i*(2x−2y)
=		=
	x2+y2		x2+y2

	2x−2y
im(v)=
	x2+y2

2x−2y
	=1⇔
x2+y2

2x−2y=x²+y² x²−2x+y²+2y=0 (x−1)²−1+(y+1)²−1=0 (x−1)²+(y+1)²=2 okrąg o środku S=(1,−1) i r=√2 bez punktu (0,0) ====================================

ite: Liczę na uścisk dłoni 🤝...

Mila: Podziwiam , że tak szybko dałaś odpowiedź, ja musiałam liczyć

ite: Też oczywiście liczyłam : )

jc:

	2+2i
Im		=1
	z

1		2+2i		2−2i
	(		−		)=1
2i		z		z*

zz^* = (1−i)z^* +(1+i)z [z−(1−i)][z*−(1+i)]=(1+i)(1−i)=2 |z−(1−i)|=√2