kwadratowa KLZ: Dla jakich wartosci rzeczywistych parametru a nierownosc x²−(a−2)x−a≤0 jest spelniona dla kazdego x∊<−1,2> taka sytuacja z warunkow zadania wynika wedlug mnie Warunki wiec takie bym dal Δ>0 x₁≥−1 i x₁≤2 i x₂≤2 x₂≥−1 Natomiast w odpowiedzi mam ze ten trojmian musi miec dwa pierwiastki x₁,x₂ takie ze x₁≤−1 i x₂≥2 Nie bardzo rozumiem dlaczego tak skoro ramiona w gore i dla x∊<−1,2> to nierownosc jest faktycznie <0

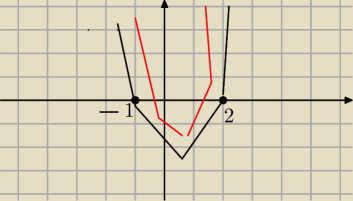
Jerzy: Zauważ,że nierowność będzie prawdziwa w tym przedziale tylko wtedy, gdy będziesz "rozchylał" ramiona tej paraboli. Na Twoim szkicu czerwona parabola nie spełnia warunków zadania.

KLZ: czyli autor zadania zaklada ze mamy sie zblizac do tego przedzialu Nie jest łatwo pojąc to jak pisze Piotr Rubik w swojej piosence Strażnik raju Że co rano słońce świeci Że świat bedzie jaki stworzą go niepoczęte jeszcze dzieci

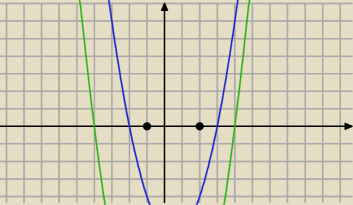
Jerzy: Te "rozchylone" parabole spełniają warunki zadania.

KLZ: Jerzy Dlaczego nie mozemy wejsc wewnatrz tego przedzialu

KLZ: Przepraszam ale czasami sie tak dlugo zastanawiam

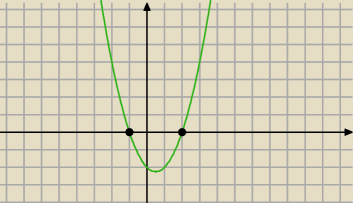
Jerzy: Popatrz na swoją czerwoną parabolę. Dla x ≈ −0,9 funkcja przyjmuje wartość dodatnią, a przecież x ≈ − 0,9 należy do przedziału <−1,2>.Podobnie jest dla np. x ≈ 1,9

KLZ: dziekuje Ci To mnie przekonalo

KLZ: To licze delte Δ=(2−a)²+4a Δ=4−4a+a²+4a Δ= a²+4 >0 dla kazdego a ∊R Teraz mam liczyc tak

	−b−√Δ
x1=		≤−1
	2

	a−2−√a2+4
x1=		≤−1
	2

a−2−√a²+4≤−2 −√a²+4≤−a √a²+4>a a²+4>a² 4>0 a∊R

	a−2+√a2+4
x2=		≥2
	2

x₂= U{a−2+√a²+4≥4 √a²+4≥6−a 6−a≥0 to a≤6 czyli a∊(−∞,6) a²+4≥(6−a)² a²+4≥36−12a+a² 12a≥32

	32		8
a≥		=
	12		3

	8		8
Wiec dla a∊(−∞,6)i a∊<		,∞) to a∊<		,6)
	3		3

	8
Biorarac wszystkie warunki to zeby byly spelnione warunki zadana to a∊<		,6)
	3

Jerzy: Chyba trochę się pospieszyłeś i niepotrzebnie napracowałeś Zauważ,że wystarczą tylko dwa warunki: 1) f(−1) < 0 2) f(2) < 0

KLZ: Wiesz . mam potem nastepne zadanie i we wskazowce jest zeby sie wzorowac na nim Wiec policzylem x₁ i x₂ Prosze sprawdz mi x₁ czy dobrze .

Jerzy: x₁ dobrze. Skad dla x₂ dałeś warunek: 6 − a ≥ 0 ? Popatrz na mój sposób: 1) f(−1) = 1 − (a − 2)(−1) − a < 0 ⇔ − 1 < 0 ( czyli nierówność prawdziwa dla dowolnego a

	8
2) f(2) = 4 − (a − 2)*2 − a < 0 ⇔ a >
	3

	8
Ostatecznie: a ∊ (		,∞)
	3

KLZ: Dalem ten warunek z ewzgledu na to zeby podniesc obie strony do potegi drugiej fakt jest mniej liczenia .

KLZ: Zle zrobilem ?

Jerzy: Podstaw a = 7 i zobaczysz, czy spełnia warunki zadania.

KLZ: a=7 nie moge podstawic bo wyszlo mi a≤6 wiec ewentualnie a=5 Sprawdze to .

Jerzy: No właśnie chcę CI pokazać,że a = 7 spełnia warunki zadania, a nie należy do zbioru Twojego rozwiązania.