Parametr KLZ: Podac wszystkie wartowsci rzeczywiste parametru a dla ktorych podana nierownosc jest prawdziwa dla wszystkich liczb rzeczywistych 1) (a−1)x²−(a−1)x+a−1>0 jesli a=1 to dostaje nierownosc liniowa −(1−1)x+1−1>0 0>0 to jest nieprawda jesli a≠1 Musi byc a−1>0 to a∊(1,∞) iΔ<0 Δ= (1−a)²−4(a−1)² Δ= 1−2a+a²−4a²+8a−4 −3a²+6a−3<0 a²+2a−1>0 (a−1)²>0 ta nierownosc jest prawdziwa dla wszystkich liczb R wiec a∊R Rozwiazanie to a∊(1,∞) Najbardziej chodzi mi o ten przypadek funkcji iniowej czy dobrze

KLZ: Terazauwazylem ma byc a²−2a+1>0

Jerzy: Cześć Dobrze, tylko trochę zapis jest nie taki. a = 1 0*x² − 0*x + 0 > 0 ⇔ 0 > 0 (sprzeczność)

Blee:

	1		1		3
(a−1)x2 − (a−1)x + (a−1) = (a−1)(x2 − x + 1) = (a−1)(x2 − 2*x*		+		+		) =
	2		4		4

= (a−1)( (x − 0.5)² + 0.75 ) > 0 dla a > 1 Tak ... tak właśnie winno się zrobić przypadek dla a=1

Jerzy: @Blee, a po co wytaczać armatę na wróbla ? Podstawiamy a = 1 i dostajemy sprzeczność,

KLZ: Witam Panow dziekuje . Bede mial jeden przyklad gdzie autor rozpatruje nierownosc liniowa

KLZ: Jerzy Wylaczyl wspolny czynnik przed nawias i x²−x+1 do postaci kanonicznej sprowadzil dla a>1 A ja tego nie zuwazylem od razu

Jerzy: Twoje rozwiązanie jest też poprawne.

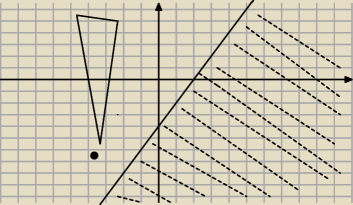
KLZ: Drugi przyklad (a−2)x²+2(2a−3)x+5a−6 <0 Dla kwadratowej zrobie bo wezme a<0 i Δ<0 Teraz dla a=2 dostaje 0x²+2x−4<0 2x−4<0 y=2x−4< 0 tak jak zaznaczylem to co pod osia Ale co z tego wynika ?

Jerzy: Czy polecenie było " dla wszystkich liczb rzeczywistych" , bo jeśli tak, to: 2x − 4 < 0 jest prawdą tylko dla x < 2

KLZ: tak dla wszystkich liczb rzeczywistych . No jasne przeciez moglem rozwiazac ta nierownosc a nie robic wykresu .

Jerzy: Czyli a = 2 nie spełnia warunków zadania

KLZ: Jerzy Czyli jak jest takie polecenie to nalezy sprawdzic co sie dzieje dla a=0

Blee: jeżeli masz nierówność ax² + bx + c < 0 (bądź >0) i masz sprawdzić dla jakich parametrów będzie to spełnione dla x∊R to: 1) sprawdzasz co się dzieje dla a = 0 1.a) jeżeli wtedy b = 0 to otrzymujesz nierówność c<0 (lub >0) i będzie to spełnione dla dowolnego x bądź będzie sprzeczne 1.b) jeżeli wtedy b ≠ 0 to od razu masz sprzeczne 2) sprawdzasz co się dzieje dla a ≠ 0 (więc masz równanie kwadratowe) Taki jest ogólny schemat

Jerzy: Lewa strona nierówności to funkcja kwadratowa, która przestaje nią być ( staje się liniową ) dla a = 2 i teraz sprawdzamy, czy ta funkcja liniowa spełnia wrunki zadania. Jeśli funkcja liniowa miałaby stałą ujemna wartość, to spełniałaby warunki tego zadania.

Jerzy: Np: (m − 1)x² + (m − 1)x + 2 > 0 dla m = 1 jest prawdziwa dla dowolnego x

KLZ: dziekuje ,dziekuje