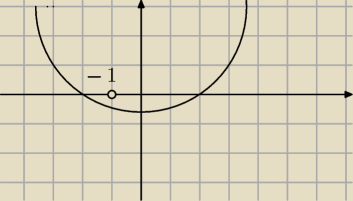
Parametr KLZ: jeden pierwiastek jest dodatni a drugi mniejszy od (−1) rownanie jest takie x²−(m−1)x+2m−5=0 Trzeba wypisac warunki Mysle 1) Δ>0 2)f(−1)<0 x₁<−1 to x₁+1<0 bedzie ujemny x₂>0 dodatni Tutaj bym dal warunek 3) x₁*x₂<0 4) x_w>−1 czy dobre ?

KLZ: Chociaz ten ostatni jest zly bo jak bedzie np x₁=−6 x₂=1 to x_w<−1 w ogole byl go nie bral pod uwage

KLZ: czy nalezy tez wziac pod uwage warunek f(0)<0?

===: zapisz porządnie treść zadania

Pan Kalafior: To znaczy że nasz wielomian ma być ujemny dla −1≤x≤0. Czyli f(−1), f(0) mają być ujemne (f(x) to ten wielomian).

Pan Kalafior: Nawet delty nie trzeba dodawać, wystarczą te warunki f(−1), f(0) < 0.

Blee: Pisząc: f(−1) < 0 de facto 'załatwiasz' warunki: Δ>0 (bo inaczej funkcja by nie przyjmowała wartości ujemnej dla x=−1) oraz x₁ < −1 ∧ x₂ > −1 (ten sam argument) Więc takie oto warunki: 1. f(−1) < 0 2. x₁*x₂ < 0 tyle wystarczy aby mieć zagwarantowane: a) dwa pierwiastki b) jeden z nich jest mniejszy od −1 c) drugi przyjmuje wartość dodatnią

KLZ: dziekuje

KLZ: Rysuje sobie sytuacje i staram sie do tego dobierac warunki Mysle ze taki sposob jest dobry === Tresc Dla jakiej wartosci parametru m i m∊R rowmamie x²−(m−1)x+2m−5=0 ma dwa rozwiazania rzeczywiste z ktorych jedno jest mniejsze od (−1) a drugie dodatnie .