Wyznacz liczbę rozwiązań równania w zależności od wartości parametru a. Mexi: a|x²−2|=x²−1

ite: a|x²−2|=x²−1 ⇒ a|x²−2|−x²+1=0

	⎧	a(−x2+2)−x2+1 gdy −√2≤x≤√2
a|x2−2|−x2+1=	⎨
	⎩	a(x2−2)−x2+1 gdy x≤−√2 lub x≥√2

i dalej trzeba pracowicie analizować w tych dwóch przedziałach Może ktoś podpowie krótszy sposób?

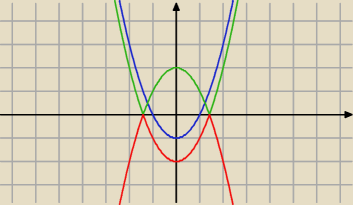
piotr: z rysunku widać, że: dla a<0 mamy 0 rozwiązań dla a>1 mamy 4 rozwiązania dla 0≤a≤1 mamy 2 rozwiązania

ite:

	−1
Geogebra podpowiada, że dla a=		istnieje jedno rozwiązanie.
	2

ite: https://www.geogebra.org/graphing/sadqukar