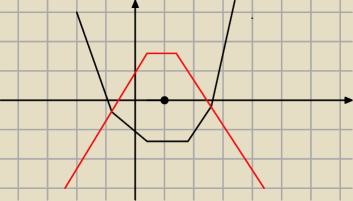
 Dla jakich wartosci parametru m liczba (1) lezy miedzy rozwiazaniami rzeczywistymi rownania
(m−4)x2−4x+m−3=0 Tutaj jakie dac warunki ?
Wydaje mi sie ze nalezy rozpatrzec osobno dla a<0 i a>0
Wiadomo ze Δmusi byc ≥0
A poza tym
Dla jakich wartosci parametru m liczba (1) lezy miedzy rozwiazaniami rzeczywistymi rownania
(m−4)x2−4x+m−3=0 Tutaj jakie dac warunki ?
Wydaje mi sie ze nalezy rozpatrzec osobno dla a<0 i a>0
Wiadomo ze Δmusi byc ≥0
A poza tym
 Dla a > 0 nałóż warunek: f(1) < 0 i odwrotnie, dla a < 0 dołóż f(1) > 0
Dla a > 0 nałóż warunek: f(1) < 0 i odwrotnie, dla a < 0 dołóż f(1) > 0
 A co z xw ? Nie rozpatrywac tego warunku ?
No bo w sumie jaki on musialby byc?
A co z xw ? Nie rozpatrywac tego warunku ?
No bo w sumie jaki on musialby byc?

| 7−√17 | ||
m1= | ≈1,44 | |
| 2 |
| 7+√17 | ||
m2= | ≈5,56 | |
| 2 |
| 7−√17 | 7+√17 | |||
Dla delty m∊< | , | > | ||
| 2 | 2 |
| 11 | ||
m< | ||
| 2 |
| 11 | ||
m> | ||
| 2 |
| 11 | ||
W odpowiedzi mam m∊(4, | ) , a ja nie bardzo rozumiem dlaczego tak jest | |
| 2 |
 m1 i m2 to z delty
Teraz jak mam zanaczyc dla m>4 i m<4 na osi liczbowej
m1 i m2 to z delty
Teraz jak mam zanaczyc dla m>4 i m<4 na osi liczbowej


 Dobrze . dziekuje .Mialem dzisiaj duzo jezdzenia bo zalatwiam papiery na rente
Konczy sie w listopadzie
Dobrze . dziekuje .Mialem dzisiaj duzo jezdzenia bo zalatwiam papiery na rente
Konczy sie w listopadzie
| 11 | ||
m∊(4, | ) | |
| 2 |
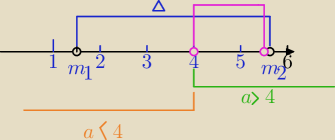 (m−4)x2−4x+m−3=0
1) Aby liczba 1 zawierała się między różnymi rozwiązaniami równania, to mogą być dwie sytuacje
jak narysowałeś 11:17.
Podam inny sposób:
a)
m−4>0 i Δ>0 i x1<1<x2⇔m>4
x1−1<0 i x2−1>0⇔
(x1−1)*(x2−1)<0⇔
x1*x2−(x1+x2)+1<0
Z wzorów Viete'a
(m−4)x2−4x+m−3=0
1) Aby liczba 1 zawierała się między różnymi rozwiązaniami równania, to mogą być dwie sytuacje
jak narysowałeś 11:17.
Podam inny sposób:
a)
m−4>0 i Δ>0 i x1<1<x2⇔m>4
x1−1<0 i x2−1>0⇔
(x1−1)*(x2−1)<0⇔
x1*x2−(x1+x2)+1<0
Z wzorów Viete'a
| m−3 | 4 | ||
−( | +1<0 | ||
| m−4 | m−4 |
| 11 | ||
⇔m∊(4, | ) ( liczba 1 między rozw.) | |
| 2 |
| 7−√17 | 7+√17 | |||
i m∊( | , | ) ( z Δ>0) | ||
| 2 | 2 |
| 7−√17 | ||
m1= | ≈1,44, m2≈5.56) | |
| 2 |
| 11 | ||
m∊(4, | ) | |
| 2 |
| 7−√17 | 7+√17 | 11 | ||||
m<4 i m∊( | , | ) i x1*x2−(x1+x2)+1<0 stąd m∊(4, | ) | |||
| 2 | 2 | 2 |


 Czy zrozumiałeś?
Czy zrozumiałeś?
