Julaa: Punkty A=(0, 4) i D=(3, 5) są wierzcholkami trapezu rownoramiennego ABCD. Podstawy trapezu są prostopadłe do prostej o równaniu x−y−6=0, do której należy punkt C. Wyznacz współrzędne pozostałych wierzchołków i oblicz jego pole.

KLZ: Prosze zrobic najpierw rysunek do zadania Skorzystaj z tego ze trapez rownoramienny ma os symetrii

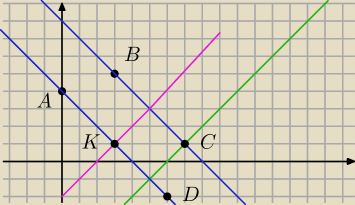
Jerzy: 1) równania prostych prostopadłych do prostej x − y − 6 = 0 , przechodzących przez A i B 2) wyznaczenie współrzednych punktu C 3) równanie symetralnej odcinka AC ( różowa) 4) równanie okregu o środku K i promieniu KA , w przecięciu z prostą AD wyznaczasz punk D

Julaa: @Jerzy punkt D jest już podany, rozwiązanie nie jest kompletne.

KLZ:

Jerzy: @Julaa , faktycznie , ale zamień na moim rysunku punkt B z punktem D i rozwiązuj dalej, Zamiast współrzędnych punktu D , szukaj współrzedne punktu B

Julaa: Punkty C=(7, 1) i B=(6, − 2) mi wyszło, ale twórca zadania podaję również drugi punkt B=(4, 0) dla którego wychodziloby, że dana figura jest rownoleglobokiem. Ale nie wiem jak do tego dojść.

Julaa: Ktoś ma jakiś pomysł?

Pitbull puppies forever!: z punktu C gdy go znajdziesz , zakreślisz o okrąg o promieniu równym odległości AB i ten okrąg przetnie prostą przechodzącą przez A w dwóch punktach, stąd dwa rozwiązania

Jerzy: Masz dobrze,a równelogłobok jest też trapezem.