 Dla jakich rzeczywistych wartosci parametru m rownanie
x2+(m−3)x−2m+6 ma dwa rozne rozwiazania rzeczywiste wieksze od 1
Mialbym taka sytuacje
warunki
1)Δ>0
(m−3)2−4[−(2m+6)]>0
m2−6m+9+8m+24>0
m2+2m+33>0
Δ<0 i m>0 to rozwiazaniem tej nierownosci sa wszystkie liczby R
m∊R
2warunek
xw=p>1
Dla jakich rzeczywistych wartosci parametru m rownanie
x2+(m−3)x−2m+6 ma dwa rozne rozwiazania rzeczywiste wieksze od 1
Mialbym taka sytuacje
warunki
1)Δ>0
(m−3)2−4[−(2m+6)]>0
m2−6m+9+8m+24>0
m2+2m+33>0
Δ<0 i m>0 to rozwiazaniem tej nierownosci sa wszystkie liczby R
m∊R
2warunek
xw=p>1
| m−3 | |
>1 | |
| 2 |
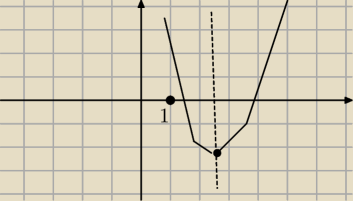
 Teraz sprawdzilem i w odpowiedzi tez mam ten 3 warunek f(1)>0
tak zastanawiam sie po co ten 3 warunek skoro ramiona paraboli w gore ?
Teraz sprawdzilem i w odpowiedzi tez mam ten 3 warunek f(1)>0
tak zastanawiam sie po co ten 3 warunek skoro ramiona paraboli w gore ?
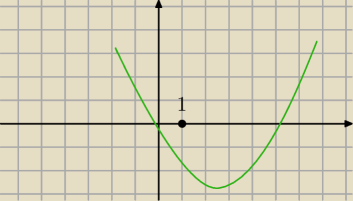 Popatrz na rysunek. xw > 1 nie gwarantuje ,ze oba pierwiastki są większe od 1
Popatrz na rysunek. xw > 1 nie gwarantuje ,ze oba pierwiastki są większe od 1
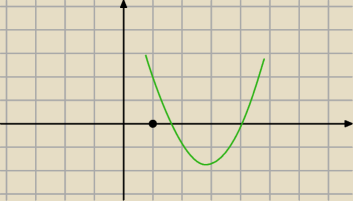 Tutaj masz dołozony warunek f(1) > 0 i to już gwarantuje,że oba są wieksze od 1
Tutaj masz dołozony warunek f(1) > 0 i to już gwarantuje,że oba są wieksze od 1
| 3−m | ||
ma byc | >1 | |
| 2 |