Liczby
adal: Hej, mam czysto teoretyczne pytanie.
Wiadomo że ujemne pierwiastki są niezdefiniowane w zbiorze liczb rzeczywistych,
dlatego np. liczba √−5 "nie istnieje" jak to się mówi na matematyce w szkole.
Ale czy taka liczba ma jakąś interpretację na liczbach zespolonych? Tzn czy mógłbym
jakies wyrażenie √−ℕ "rozwiązać" w postaci zespolonej?
Z góry dzięki za pomoc
16 paź 22:32
KLZ: i2=−1
√i25=√i2*√5= i√5
16 paź 22:35
Zespolony:
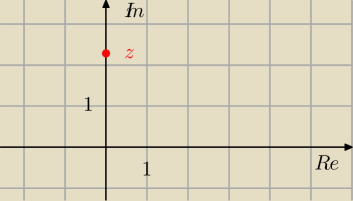√−5=i
√5
z=i
√5⇒ Re(z)=0 oraz Im(z)=
√5
zatem jest to punkt o współrzędnych (0,
√5)
16 paź 22:38
ABC:
zaraz ktoś wam powie, że pierwiastek zespolony to zbiór
√−5={−i
√5, i
√5}
16 paź 22:41
adal: A czy np rownianie |x−3|= −2 też mógłbym rozwiązać w analogiczny sposób?
16 paź 22:57
KLZ: Nie
|x−3| zawsze jest ≥0
16 paź 22:58
adal: Albo sytuację gdzie Δ<0, wiec nie przecina osi X. Jednak czy w zespolonej interpretacji da się
to jakos policzyć?
16 paź 23:00
KLZ: Da sie w zespolonej gdy Δ<0
16 paź 23:01
Pan Kalafior: ABC, ty też z kontrwywiadu?
18 paź 00:59