Zaznaczyć na płaszczyźnie zespolonej zbiory punktów spełniających warunki:
kajtek138824: Zaznaczyć na płaszczyźnie zespolonej zbiory punktów spełniających warunki:
Bardzo proszę choćby o nakierowanie jak zaznaczyc takie cos na płaszczyznie.
1. |z − 3 + 4i| = 1
2. |z(sprzezenie(kreska nad z)) + 2 − i| <=|z|
16 paź 19:37
Mila:
|z−z0|=1 − zbiorem punków jest okrąg o środku z0 i r=1
1)
|z−(3−4i)|=1
okrąg o środku S=(3,−4) i promieniu r=1
− możesz też rozwiązać tak:
z=x+iy, gdzie x,y∊R
|x+iy−3+4i|=1⇔
|(x−3)+i*(y+4)|=1⇔
√(x−3)2+(y+4)2=1 /2
(x−3)2+(y+4)2=1 − równanie okręgu o środku S=(3,−4) i promieniu r=1
16 paź 20:01
PW: Nakierowanie:
|z − w|
to odległość między punktem z = (x, y) a w = (x0, y0) na płaszczyźnie kartezjańskiej:
Jeżeli z = x + iy oraz w = x0 + iy0, to
|z − w| = |(x − x0) + i (y − y0)| = (def) = √(x − x0)2 + (y − y0)2.
16 paź 20:04
Mila:
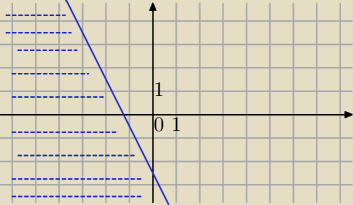
2) |z
*+2−i|≤|z|
z=x+iy, gdzie x,y∊R
|x−iy+2−i|≤|x+iy|
|(x+2)+i*(−y−1)|≤|x+iy|
√(x+2)2+(−y−1)2≤
√x2+y2 /
2
(x+2)
2+(y+1)
2≤x
2+y
2
x
2+4x+4+y
2+2y+1≤x
2+y
2
4x+4+2y+1≤0
4x+2y+5≤0
2y≤−4x−5
| | 5 | | 5 | |
y≤−2x− |
| zbiór punktów na prostej y=−2x− |
| i pod tą prostą |
| | 2 | | 2 | |
16 paź 20:09
kajtek138824: Bardzo dziękuję za pomoc.
17 paź 13:07
jc:
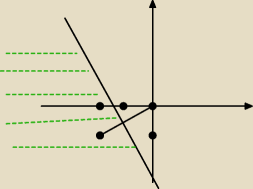
|z
* + 2 − i| ≤ |z|
|z + 2 + i| | ≤ |z|
Punkty leżące po jednej stronie symetralnej odcinka łączącego 0 z (−2−i).
17 paź 16:43
 2) |z*+2−i|≤|z|
z=x+iy, gdzie x,y∊R
|x−iy+2−i|≤|x+iy|
|(x+2)+i*(−y−1)|≤|x+iy|
√(x+2)2+(−y−1)2≤√x2+y2 /2
(x+2)2+(y+1)2≤x2+y2
x2+4x+4+y2+2y+1≤x2+y2
4x+4+2y+1≤0
4x+2y+5≤0
2y≤−4x−5
2) |z*+2−i|≤|z|
z=x+iy, gdzie x,y∊R
|x−iy+2−i|≤|x+iy|
|(x+2)+i*(−y−1)|≤|x+iy|
√(x+2)2+(−y−1)2≤√x2+y2 /2
(x+2)2+(y+1)2≤x2+y2
x2+4x+4+y2+2y+1≤x2+y2
4x+4+2y+1≤0
4x+2y+5≤0
2y≤−4x−5
 |z* + 2 − i| ≤ |z|
|z + 2 + i| | ≤ |z|
Punkty leżące po jednej stronie symetralnej odcinka łączącego 0 z (−2−i).
|z* + 2 − i| ≤ |z|
|z + 2 + i| | ≤ |z|
Punkty leżące po jednej stronie symetralnej odcinka łączącego 0 z (−2−i).