FDSFDS Burczyk: Jak zaznaczyć taki obszar w układzie współrzędnych? 2 ≤ | i*z − 5 | < 3

ABC: chcesz to zrozumieć czy chcesz gotowca?

Burczyk: Zrozumieć. Dopiero zacząłem zabawę z liczbami zespolonymi.

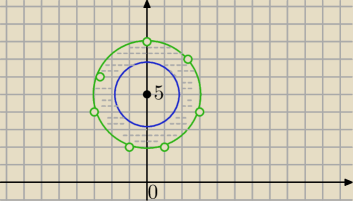
PW: Jeżeli z = x + iy. to iz = i(x + iy) = ix + i² y = −y + ix, zatem iz − 5 = −(y+5) + ix |iz − 5| = √(y+5)² + x², a więc zadana nierówność ma postać 2 ≤ √(y+5)² + x² ≤ 3, równoważnie 2² ≤ x² + (y+5)² ≤ 3². Pierścień kołowy (z brzegami).

jc: Skorzystaj z ważnej własności modułu: |zw|=|z| |w|

PW: Oj, a ja tymczasem gotowca ze zrozumieniem.

ABC: A ja chciałem wyjść od 2≤|z−5|<3 jako łatwiejszego do wyobrażenia sobie pierścienia i przejść przez interpretację geometryczną mnożenia przez i , ale jak PW napisał to i lepiej

Burczyk: Dzięki, zaraz będę analizował

PW: Mówiłeś, że dopiero zaczynasz, więc dałem wersję dla początkujących. Warto jednak przemyśleć wersję podpowiedzianą przez jc − krótka i skuteczna.

Mila: 2 ≤ | i*z − 5 | < 3⇔ 2≤ |iz+5i²|<3 2≤|i|*|z+5i|<3 2≤|z+5i|<3 S=(0,−5) , r₁=2,r₂=3

Mila: S=(0,−5) Poprawisz sam rysunek?