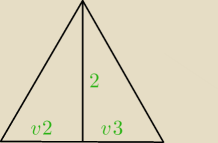
 W trójkącie ABC poprowadzono wysokość CD równą 2. Punkt D podzielił bok AB na takie odcinki, że
|AD| = √2, |BD| = √3.
Oblicz sinus kątka ACB
(przy wysokości kąt prosty)
Wierzchołek A na dole po lewej, B po prawej, C u góry
W trójkącie ABC poprowadzono wysokość CD równą 2. Punkt D podzielił bok AB na takie odcinki, że
|AD| = √2, |BD| = √3.
Oblicz sinus kątka ACB
(przy wysokości kąt prosty)
Wierzchołek A na dole po lewej, B po prawej, C u góry
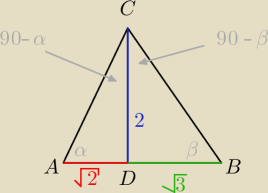 my szukamy
sin(90−α+90−β)=sin(180−(α+β))=sin(α+β)=sinα*cosβ+cosα*sinβ
a te funkcje już łatwo obliczyć
my szukamy
sin(90−α+90−β)=sin(180−(α+β))=sin(α+β)=sinα*cosβ+cosα*sinβ
a te funkcje już łatwo obliczyć
| 1 | ||
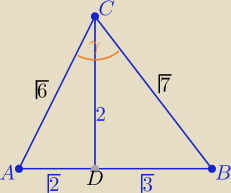
P(ABC)=(√2+√3) i P(ABC)= | *√6*√7*sinγ | |
| 2 |
 Z kolei z pierwszego sposobu wyszedł mi inny wynik, czy mogłabym prosić o pomoc w wyliczeniu
tej funkcji?
Niestety do obu rozwiązań doszłam sama, jednak leże na poziomie samych obliczeń
Z kolei z pierwszego sposobu wyszedł mi inny wynik, czy mogłabym prosić o pomoc w wyliczeniu
tej funkcji?
Niestety do obu rozwiązań doszłam sama, jednak leże na poziomie samych obliczeń
| 2(√2+√3) | ||
sinγ= | ||
| √42 |