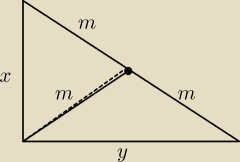
Trojkąt KLZ: Polowa obwodu trojkata prostokatnego jest rowna p Srodkowa przeciwprostokatnej jest rowna m Oblicz przyprostokatne Podaj warunki rozwiazywalnosci zadania x+y+2m=2p x²+y²=(2m)² x=2p−y−2m (2p−y−2m)²+y²= 4m² 4m²−8mp+4my+4p²−4py+y²+y²= 4m² 2y²+4my−4py +4p²−8mp=0 2y²+y(4m−4p)+4p²−8mp=0 Δ=(4m−4p)²−4*2(4p²−8mp) Δ=16m²−32mp+16p²−32p²+64mp Δ= 16m²−16p²+32mp Δ=m²−p²+2mp zeby bylo m²+2mp +p² to bylby wzor skrocenego mnozenia Teraz liczyc y₁ i y₂?

KLZ:

PW: Środkowa przeciwprostokątnej ma długość m, ale dlaczego sądzisz, że przeciwprostokątna ma długość 2m?

KLZ: @PW we wskazowce do zadania mam tak zaznaczone

KLZ: srodkowa dzieli trojkat prostokatny na dwa trojkaty rownoramienne

PW: Tak, przekątne prostokąta są tej samej długości i połowią się, więc jest to prawda, ale wypadałoby o tym napisać.

KLZ: Ten pierwszy uklad czyli {x+y+2m=2p {x²+y²=(2m)² zgadza sie podpowiedzia jednak ja nie zapisalem warunkow

	1
x>0 y>0 i 0<m<		p czyli m>0 musi byc to logiczne
	2

	1
i m<		p skad taki warunek ?
	2

PW: Z nierówności trójkąta 2m < x + y, a więc 4m < x + y + 2m 4m < 2p

	p
m <
	2

KLZ: Δ=m²+2mp−p² wyszla mi taka jak w odpowiedzi Zeby bylo 1 rozwiazanie to Δ=0 i m>0 m²+2mp−p²=0 Δ=4p²+4p² Δ= 8p² √Δ= 2√2p

	−2p−2√2p		2(−p−√2p
m1=		=		=−p−√2p=p(−1−√2) Odpada bo −1−√2<0
	2		2

m₂=p(√2−1)

	1
czyli 0<p(√2−1)<		p
	2

Jak mam teraz wyliczyc x i y ?

KLZ: Jest ktos w stanie sensownie pomoc ?

Mila: Dla m=p*(√2−1) − nie sprawdzałam tego, ale piszesz, że to zgodne z odpowiedzią?

	2p		2p
x=		, y=		tu taka jest odpowiedź?
	2+√2		2+√2

KLZ: m=p(√2−1) tak zgodne z odpowiedzia wtedy x=y = p(2−√2) tak mam w odpowiedzi .

Eta: Usuń niewymierność w tym co podała Mila i po "ptokach"

Mila: No to jest to samo, bo

	p*(2−√2)		2+√2		p*(4−2)
x=		*		=
	1		2+√2		2+√2

	2p
x=y=
	2+√2

KLZ: Jak obliczylas x ?

KLZ: Natomiast dla Δ>0 i m>0 to juz w ogle nie rozumiem jak wyliczyc x i y tutaj m∊(p(√2−1),∞) ze wzgledu na warunek m>0

Mila: Z układu x+y=2(p −m) x²+y²=(2m)2 −−−−−−−−−−− x+y=2*(p−p(√2−1)⇔x+y=4p−2√2 i x²+y²=4(√2−1)² x+y=2p*(2−√2) x²+y²=4(√2−1)² −−−−−−−−−−−−−− y=2p(2−√2)−x x²+4p²*(2−√2)²−4p*(2−√2)*x+x²=4(√2−1)² 2x²−4p*(2−√2)*x+4p²*[(2−√2)²−(√2−1)²)]=0 x²−2p(2−√2*x+2p²(3−2√2)=0 Δ=0 x i y jw.

Mila: Ja rozwiązałam układ dla m=p*(√2−1) Jutro pomyślimy co dalej Dobrze?

KLZ: Dobrze . Na razie dziekuje . Jutro wstawie skan z rozwiazaniem z ksiazki

KLZ: https://zapodaj.net/0be493b6476ee.jpg.html https://zapodaj.net/f1e6c0e6b21fd.jpg.html Zadanie nr 265 .

KLZ: poczatek drugiego skanu

	1
p(√2−1)<m<		p⇒ itd
	2

KLZ: Chcialbym sie przypomniec .

PW: Ale o co idzie? Masz kompletne rozwiązanie w książce i domagasz się kogoś, kto "jest w stanie sensownie pomóc".

KLZ: Dobry wieczor . A nie przyszlo CI czasani do glowy to ze nie rozumiem tego rozwiazania ?

PW: To nie bierz się za takie trudne zadania, zacznij od łatwiejszych. Skąd wiara, że na forum ktoś wytłumaczy lepiej niż w książce?

Eta: To zadanie sprzed 50 laty Dziś nikt nie męczy ludzi takimi zadaniami, bo 90% licealistów nie uzyskałaby matury! "małolat" tak ma, że lubi się katować!

PW: Eta, to chyba nie jest małolat (nie ta kultura wypowiedzi).

Eta: Na 100% "małolat" ( ostatnio bardzo się zmienił na ........

Mila: Δ>0⇔są dwa rozwiązania: ograniczenia masz podane: x+y=2(p −m) x²+y²=(2m)² y=2(p−m)−x x²+(2(p−m)−x)²=4m² x²+4(p−m)²−4x(p−m)+x²−4m²=0⇔ 2x²+4*(p²−2pm+m²)+4x(p−m)−4m²=0 2x²+4x*(p−m)+4p²−8pm=0 /:2 x²−2(p−m)x+2p²−4pm=0 Δ=4(p−m)²−4*(2p²−4pm)⇔Δ=4m²+8pm−4p² Δ=4*(m²+2pm−p²)

	2(p−m)−2√m2+2pm−p2
x1=		=p−m−√m2+2pm−p2
	2

lub x₂=p−m+√m²+2pm−p² x=x₁, y=x₂ albo na odwrót podstaw x₁ do wzoru y=2(p−m)−x to tak wyjdzie.

KLZ: dziekuje

Mila: