funkcje
Nikto0: Witam. Nie wiem jak rozwiązać zadanie 300.
https://zapodaj.net/b5e43aad13b49.jpg.html
Odpowiedź do zadania to podpunkt a). Wiem że
x−2/x+2 jest większe bądź równe 0 i że z dziedziny odpada 2 i minus 2.
14 paź 18:12
Maciess: Cała ta wartosc pod pierwiastkiem musi byc ≥0
14 paź 18:14
Jerzy:
Przed ustalaniem dziedziny nie wolno dokonywać żadnych uproszczeń.
14 paź 18:15
Nikto0: Maciess właśnie tak liczyłam do momentu w którym x−2/x+2 jest większe bądź równe zeru
14 paź 18:19
Jerzy:
No to pokaż te rachunki.
14 paź 18:20
Maciess: Czyli musisz rozwiązać nierówność
(x−2)(x+2)≥0
Nie wiesz jak to zrobić?
14 paź 18:22
6latek: | 8−4x | | 8−4x+x2−4 | | x2−4x+4 | |
| +1= |
| = |
| |
| x2−4 | | x2−4 | | x2−4 | |
wiec
| | x2−4x+4 | |
bedzie tak x2−4≠0 i |
| ≥0 |
| | x2−4 | |
14 paź 18:23
14 paź 18:27
Jerzy:
| | x2 − 9 | |
Pytanie do Nikto0 , jaka jest dziedzina funkcji: y = |
| |
| | x − 3 | |
14 paź 18:28
Nikto0: Rzeczywiste oprócz trójki
14 paź 18:30
Jerzy:
Ano właśnie. Przed ustaleniem dziedziny nie wolno nam zapisać: y = x + 3 , bo dzidziną tej
funkcji jest R
14 paź 18:33
Jerzy:
Dlaczego dla mianownika wyeliminowałaś tylko x = −2 ?
14 paź 18:37
14 paź 18:40
Jerzy:
(x + 2)(x − 2) ≥ 0 ⇔ x ∊(−∞,−2] U [2,∞)
14 paź 18:42
Jerzy:
Jest już dobrze, z tego co napisałem wyżej, usuwasz: −2 i 2
14 paź 18:43
Nikto0: Dziękuję

14 paź 18:45
15 paź 12:01
Jerzy:
Możesz ,tylko po co komplikować sobie życie. f(x) = (x − 2)(x + 2)i widać,że miejsca zerowe tej
funkcji, to x = −2 lub x = 2 i gałęzie skierowane do góry, czyli f(x) ≥ 0 ⇔ x ∊ (−∞,2] U [2,∞)
15 paź 12:05
Jerzy:
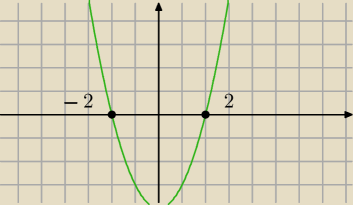
15 paź 12:07
Nikto0: Tylko nie wiem dlaczego mi nie wychodzi wynik. Jak to zrobić tym sposobem?
15 paź 12:08
Nikto0: Tym moim tamten znam
15 paź 12:09
Jerzy:
x − 2 ≥ 0 i x + 2 ≥ 0 ⇔ x ≥ 2 i x ≥ −2 ⇔ x ≥ 2 ⇔ x ∊ [2,∞)
x − 2 ≤ 0 i x + 2 ≤ 0 ⇔ x ≤ 2 i x ≤ −2 ⇔ x ≤ − 2 ⇔ x ∊ (−∞,−2]
15 paź 12:13
Jerzy:
Poza tym twój lewy rysunek jest zly. Na osi liczbowej liczba −2 leży na lewo od liczby 2.
15 paź 12:16
Nikto0: Dziękuję.
15 paź 12:29

